高中数学必修二：第七章复数_思维导图模板

高中数学必修二：第七章复数

作者：TeacherR

0浏览2024-04-28 10:13:58

下载

使用模板已被用1次

复数

7.1 复数的概念

数系的扩充和复数的概念

形如 a + b（a，b∈R）的数称为复数，其中叫做虚数单位，全体复数构成的集合C={ a + b | a，b∈R}叫做复数集

复数通常用表示，即 = a + b，其中a与b分别叫做复数Z的实部与虚部

复数相等

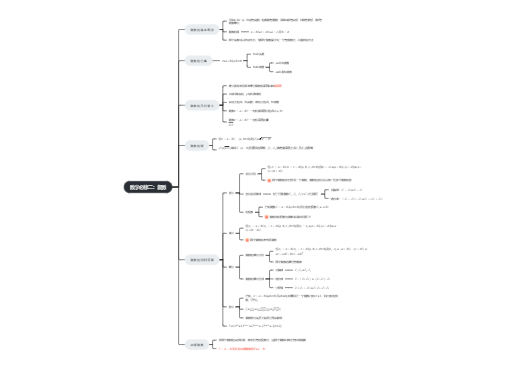
= ⇔ ，且

复数的分类

= + （，∈R ）

=0，值为实数

a=0，b=0，值为0

b≠0，a≠0，值为虚数

b≠0，a=0，值为纯虚数

复数的几何意义

点Z的横坐标是a，纵坐标是b，复数 = a + b可用点Z（a，b）表示，这个建立直角坐标系来表示复数的平面叫做复平面，x轴叫做实轴，y轴叫做虚轴，实轴上的点，纯实数；虚轴上的点，纯虚数

复数一一对应复平面内的点

复数一一对应平面向量

为方便起见，我们常把复数＝a＋b 说成点Z或说成向量，并且规定，相等的向量表示同一个复数．

向量的模叫做复数的模，或绝对值，记作| |或 | a+b |，即| | = | a+b | = ，其中a，b∈R

如果b=0，那么= a + b 是一个实数a，它的模就等于| a | （a的绝对值）

共轭复数

当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数，虚部不等于０的两个共轭复数也叫做共轭虚数

的共轭复数为

7.2 复数的四则运算

复数的加、减运算及其几何意义

加法

加法法则

设：， (∈R)，则=( )+( )=+

两个复数的和仍然是一个复数，类似于两个多项式相加，复数的加法可以推广到多个复数相加

加法的运算律

减法

减法法则

设：， (∈R)，则=()-()=+

两个复数的差也是复数，类似于两个多项式相减

复数的差的模表示两个复数之间的距离

复数的乘除运算

乘法

复数的乘法法则

设：， (∈R)，则=（）（）=

两个复数的乘仍为复数，类似于两个多项式相乘

复数的乘法定律

除法

除法法则

已知， (a，b∈R，且≠0)，如果存在一个复数z'使z·z'=1，则z'是z的倒数，记作

===

复数除法实质上就是分母实数化

复数的倒数与共轭复数辐射角度相同

7.3 复数的三角表示

复数的三角表示式

一般地，任何一个复数都可以表示成的形式，其中r是复数的的模，θ是以x轴的非负半轴为始边，所在射线（射线OZ）为终边的角，叫做复数的辐角，r（cosθ+i sinθ）叫做复数三角表示式，简称三角形式，为了与三角形式区分开来，叫做复数的代数形式，简称代数形式

复数的辐角为，规定范围内的辐角θ的值为辐角的主值，通常记作arg

复数乘、除运算的三角表示及其几何意义

两个复数相乘，积的模等于各复数的模的积，积的辐角等于各复数的辐角的和．

两个复数相除，商的模等于被除数的模除以除数的模所得的商，商的辐角等于被除数的辐角减去除数的辐角所得的差．

查看详情

模板简介

高中数学必修二：第七章复数，同步教材知识点，后续持续更新

高中数学必修二第七章复数复数同步教材知识点

举报/反馈

您的想法与建议，对知犀思维导图的优化改进非常有用！欢迎反馈！