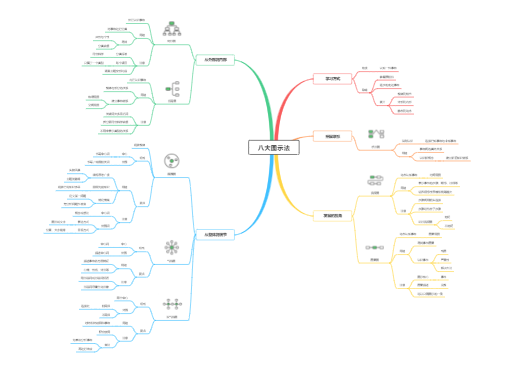
两个数相除又叫做两个数的比
“:”是比号,读作“比”。比号前面的数叫做比的前项,比号后面的数叫做
比的后项。比的前项除以后项所得的商,叫做比值
同除法比较,比的前项相当于被除数,后项相当于除数,比值相当于商
比值通常用分数表示,也可以用小数表示,有时也可能是整数
比的后项不能是零
根据分数与除法的关系,可知比的前项相当于分子,后项相当于分母,比值相当
于分数值
比的前项和后项同时乘或者除以相同的数(0除外),比值不变
用比的前项除以后项,它的结果是一个数值可以是整数,
也可以是小数或分数
根据比的基本性质可以把比化成最简单的整数比,它的结果
必须是一个最简比,即前、后项是互质的数
在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行
分配。这种分配的方法通常叫做按比例分配
首先求出各部分占总量的几分之几,然后求出总数的几分之几是多少
表示两个比相等的式子叫做比例
组成比例的四个数,叫做比例的项。两端的两项叫做外项,中间的两项叫做内项
判断两个比能不能组成比例,关键要看它们的比值是不是相等,若比值相等,则能组成比例;
若比值不相等,则不能组成比例
比例中等号的两侧必须都是一个比
把等式ax=by改写成比例式后,a和x必须同时为外项,或同时为内项
在比例里,两个外项的积等于两个两个内项的积
如果ab=cd,那么a:d与c:b能组成比例
比表示两个量相除的关系,它有两项(即前、后项);
比例表示两个比相等的式子,它有四项(即两个内项和两个外项)
比有基本性质,它是化简比的依据;比例也有基本性质,它是解比例的依据
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应
的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关
系叫做正比例关系。用字母表示x/y=k(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应
的两个数的积一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关
系。用字母表示xy=k(一定)
看这两个相关联的量中相对就的两个数的商一定还是积一定,如果商一
定,就成正比例;如果积一定,就成反比例
都是两种相关联的量
一种量随着另一种量变化
“变化方向”相同,一种量扩大或缩小,另一种量也扩大或缩小
相对应的两个数的比值(商)一定
关系式:x/y=k(一定)
“变化方向”相反,一种量扩大或缩小,另一种量反而缩小或扩大
相对应的两个数的乘积一定
关系式:xy=k(一定)
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺
比例尺是一个比,因此不能带有计量单位
比例尺是图上距离比实际距离得到的最简整数比,可以写成带比号的形式,也可以写成分数形式
在大小相同的地图上,比例尺越大,反映的实际范围越小
线段比例尺可以改写成数值比例尺
改写方法:根据线段比例尺,写出图上距离和实际距离
的比,统一单位后再化成最简比的形式
通常缩小比例尺的前项为1,放大比例尺的后项为1
图上距离÷实际距离=比例尺
实际距离×比例尺=图上距离
图上距离÷比例尺=实际距离
写出图的名称
确定比例尺
根据比例尺求出图上距离
画图(画出单位长度)
标出实际距离,写清地点名称
标出比例尺
保持图形原来的形状而使图形变小,叫做图形的缩小;
保持图形原来的形状而使图形变大,叫做图形的放大
图形放大或缩小后所得到的图形与原图形相比,形状相同,大小不同
单价×数量=总价
单产量×数量=总产量
速度×时间=路程
工效×工作时间=工作总量