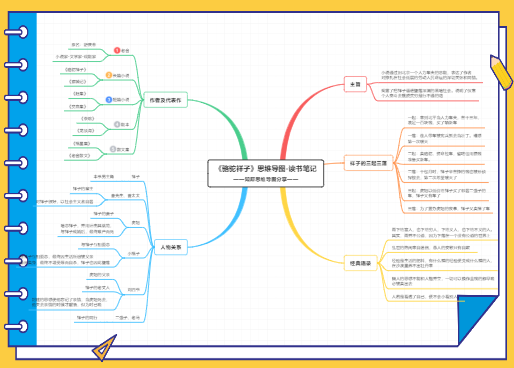
方程中只含有两个未知数
所含未知数的项的次数都为1
方程是整式方程
方程组中只含有两个未知数
所含未知数的项的次数都为1
方程是整式方程
一般地,使二元一次方程两边的值都相等的两个未知数的值,叫做元一次方程的解
二元一次方程有无数个解
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解
一般情况下,一个二元一次方程组只有唯一的一组解;二元一次方程组的解还有另外两种情况:无解或有无数组解
把二元一次方程组中的一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法。
1.变形(选系数简单的方程变形)
2.代入
3.求解
4.回带
5.写解(用“{”将未知数的值联立起来)
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个元一次方程。这种方程叫做加减消元法,简称加减法。
1.变形(使方程中某一个未知数的系数相等或互为相反数)
2.加减(转化为一元一次方程)
3.求解
4.回带
5.写解
审:弄清题意和题目中的等量关系,用字母表示题中的两个未知数
设:找出题目中的两个等量关系
列:根据找出的两个等量关系列出方程组
解:解方程组
验:检验所得的解是否是方程组的解,检验是否符合题意
答:写出答案(包括单位)
含有三个未知数,所含未知数的项的次数都是1,这样的方程叫做三元一次方程。
含有三个未知数,每个方程中含有未知数的项的次数都是1,并且共含有三个方程,像这样的方程组叫做三元一次方程组。
1.含有三个未知数
2.每个方程中含未知数的项的次数都是一
3.是整式方程组
三元一次方程组中各个方程的公共解,叫做这个三元一次方程组的解。
判断一组数中是否为三元一次方程组的解时,将各数代入三个方程若三个方程均成立,则这组数是该方程组的解。
通过“代入”或“加减”进行消元,把“三元”化为“二元”,使三元一次方程组转化为解次方程组,再转化为解一元一次方程组。
1.用代入或加减法把方程组中一个方程与另外两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元次方程组。
2.解这个二元一次方程组,求出两个未知数的值
3.将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程
4.解这个一元次方程,求出最后一个未知数的值
5.将求得的三个未知数的值用“{”联立起来