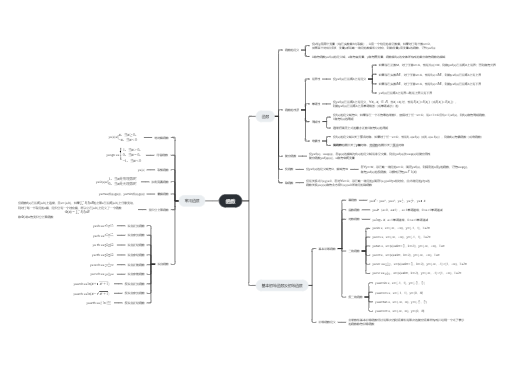
含有未知数函数的导数
通解
初值条件
y'=f(x,y)
y'=ɸ()
齐次线性方程
常数变易法
对应的齐次方程通解+非齐次方程的一个特解之和
=f(x)
y''=f(x,y')
y''=f(y,y')
f(x)=0——齐次方程
f(x)≠0——非齐次方程
λ是特征方程的k重根(k取0,1,2)
[coswx+sinwx]
m指的是次方数,m=max{l,n}
λ+iw为特征方程的k重根
n阶常系数齐次线性微分方程
将对应常系数线性微分方程的阶数换成对应的幂次数,得到的方程称为微分方程的特征方程
对于二阶齐次线性微分方程y''+P(x)y'+Q(x)y=0,如果(注意不一定为通解)
当定理一中的
是两个线性无关的解,是方程的通解
如果是n阶齐次线性方程
=0的n个线性无关的解,则此方程的解为,
非齐次线性方程通解等于对应的齐次方程通解加非齐次方程的特解
设非齐次线性方程右端为两个函数之和y''+P(x)y'+Q(x)y=;与fe分别是方程y''+P(x)y'+Q(x)y=和方程y''+P(x)y'+Q(x)y=的特解;则是原方程的特解
(x),(x)...,(x)为定义在区间I上的n个函数,如果存在n个不全为0的常数,,,使得,则称这n个函数在区间I上线性相关,否则称线性无关