六上数学思维导图_思维导图模板

六上数学思维导图

分数乘法

分数乘法意义

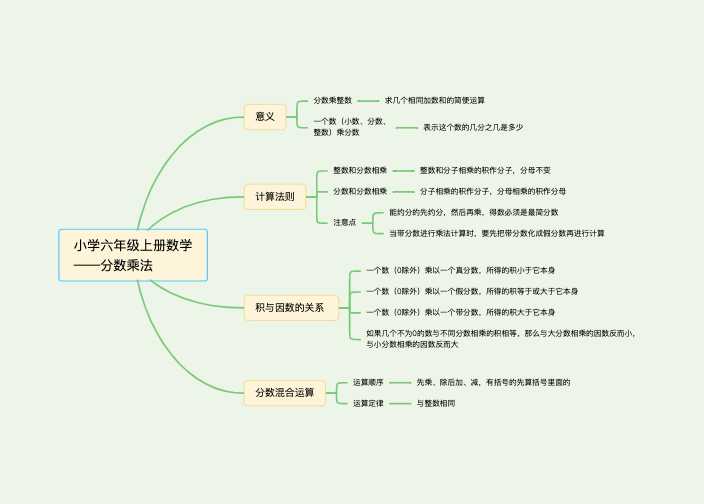
1.分数乘整数的意义和整数乘法的意义完全相同，就是求几个相同加数的和的简便运算

2.一个数乘整数的意义就是求一个数的几分之几是多少

分数乘法计算法则

1.分数乘整数的计算法则是：分子与整数相乘，分母不变

2.单位1通常在”是“”比“”占“后

积与因数的关系

1.1个数（0除外）乘大于1的数，积大于这个数

2.1个数（0除外）乘等于1的数，积等于这个数

3.1个数（0除外）乘小于1的数，积小于这个数

分数乘法混合运算

1.分数乘法混合运算顺序与整数相同，先乘除，后加减，有括号的先算括号里的，再算括号外的。括号有三种：“{}”叫做大括号；“[]”叫做中括号；“（）”叫做小括号，运算时应遵循“先小后中再大”

2.整数乘法运算定律对分数乘法同样适用，运算定律可以使一些计算简便。

1.乘法交换律：axb=bxa

2.乘法结合律：（axb）xc=ax（bxc）

3.乘法分配律：ab+ac=a(b+c)

倒数的意义

1.乘积为1的两个数互为倒数

2.倒数是两个数的关系，它们相互依存，不能单独存在

3.判断两个数是否互为倒数的方法是：两数相乘的积是否等于1

4.1的倒数是它本身，0没有倒数

5.任意数a（a≠0）它的倒数是a分之1

6.真分数的倒数>1 假分数的倒数小于或等于1

7.求倒数的方法

1.求分数的倒数：交换分子和分母的位置

2.求整数的倒数：整数分之一

3.求带分数的倒数：先化成假分数，再求倒数

4.求小数的倒数：先化成分数再求倒数

甲比乙（多）少多少

1.多：（大-小）÷单位1

2.少：（大-小）÷单位1

分数除法

1.分数除法计算法则

1.除以一个(0除外),等于乘上这个数的倒数

2.被除数÷除数=被除数x除数的倒数

3.分数除法中如果出现小数，带分数，需要先将它们化成分数再计算

4.被除数与商的变化规律

1.除以大于一的数，商小于被除数

2.除以小于一的数，商大于被除数(0除外）

3.除以等于一的数，商等于被除数

2.分数除法混合运算顺序

1.连除

2.先乘除，后加减，有括号的先算括号里面的

3.比

1.比式中，比号（：)前面的数叫做前项，后面的数叫做后项，比号相当于除号，比的前项除以后项的值叫做比值。

2. 两个数相除也叫两个数的比

3.比的基本性质：比的前项和后项同时乘或除以一个相同的数(0除外）比值不变

4.化简比

1.化简之后，还是一个比，不是一个数

2.用比的前项和比的后项同时除以它们的最大公因数，比值不变

3. 两个分数的比用前项后项同时乘分母的最小公倍数，再按化简比的方法来化简，也可以求出比值再写成比的形式

4. 两个小数的比，向右移动小数点的位置，也是先化成整数比

5.求比值：把比号画成除号再计算，结果是一个整数或分数或小数，相当于商，不是比。

4.分数除法的应用

1.已知单位1用乘法

2.求单位1用除法

3.多就1+

4.少就1-

圆的初步认识

圆的认识

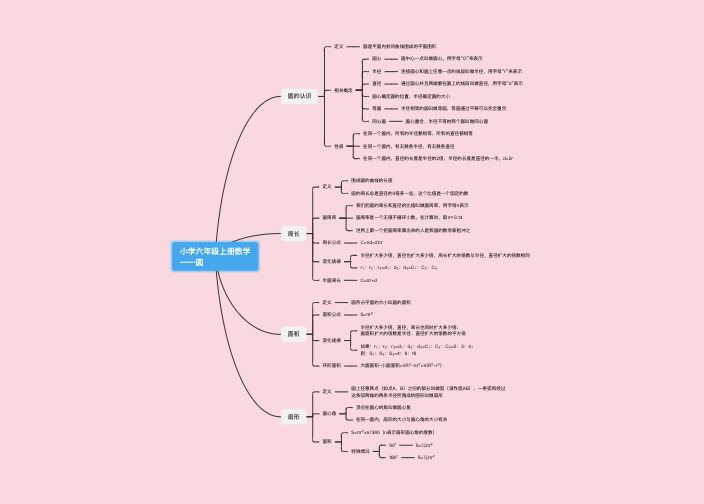
圆心o：圆中心的点叫圆心，圆心确定圆的位置

半径r：连接圆心到圆上任意一点的线段叫做半径，在同一个圆里，有无数条半径，且所有的半径相等。重点：半径确定圆的大小

直径d：通过圆心且两端都在圆上的线段叫做直径，在同一个圆里，有无数条直径，且所有的直径相等。重点：直径是圆内最长的线段

圆的周长

1.周长c 公式=2πr=πd

2.圆周率：圆的周长和直径的比值是一个固定值，叫做圆周率，用字母π表示

3.周长变化的规律

半径扩大多少倍，周长和直径也扩大多少倍，圆面积扩大的倍数是半径，直径的倍数的平方倍

4.半圆形周长：πd÷2+d=2πr÷2+d=πr+d

5.跑道周长：2πr＋两条直跑道的和

圆的面积

1.s面=πr²

2.几种图形在面积相等的情况下，圆的周长最短，而长方形的周长最长；反之，在周长相等的情况下，圆的面积最大，长方形面积最小

3.其它图形面积

1.圆环：πx（R²-r²）

2.扇形：πr²x360n（n表示圆心角的度数）

4.任何一个正方形最大的内切圆及最大的直径是正方形的边长，它们的面积比是4：π

百分数

1.百分数的意义

1.表示一个数是另一个数的百分之几

2.百分数是专门用来表示一种特殊的倍比关系的，表示两个数的比，所以，百分数又叫百分比或百分率

3.百分数和分数的区别与联系

1.联系：都可以用来表示两个数的倍比关系

2.区别：意义不同：百分数只表示倍比关系，不表示具体数量，所以不能带单位。分数不仅表示倍比关系，还能带单位表示具体数量。百分数的分子可以是小数，分数的分子只能是整数

4.小数，整数，百分数之间的互化

1.百分数化小数：小数点向左移动两位，去掉“％”

2.小数化百分数：小数点向右移动两位，填上“％”

3.百分数化分数:先把百分数写成分母是100的分数，然后再化简成最简分数.

4.分数化百分数:分子除以分母得到小数，(除不尽的保留三位小数）然后化成百分数。

5.小数化分数:把小数成分母是10、100、1000等的分数再化简

6.分数化小数:分子除以分母

2.百分数的应用

1.求常见的百分率如:达标率、及格率、成活率、发芽率、出勤率等求百分率就是求一个数是个数的百分之几

2.求一个数比另一个数多或少百分之几，实际生活中，人们常用增加了百分之几，减少了百分之几，节约了百分之几等来表示增加或减少的幅度

3.求一个数的几分之几是多少一个数（单位1）x百分率

4.已知一个数的百分之几是多少，求这个数部分量÷百分率=一个数(单位“1”)

5.折扣折扣、打折的意义:几折就是十分之几也就是百分之几十

6.纳税:缴纳的税款叫做应纳税额

1.应纳税额÷总收入=税率

2.应纳税额=总收入x税率

7.利率

(1)存入银行的钱叫做本金。

(2)取款时银行多支付的钱叫做利息。

(3)利息与本金的比值叫利率

8.基本公式

1.利息=本金x利率x时间

2.税后利息=利息-利息的应纳税额=利息-利息x5%

9.百分数应用题型分类

1.求甲是乙的百分之几 (甲÷乙) x100% =甲/乙 x100%= 百分之几

2.求甲比乙少多几分之几差/比字后面x100％=差/乙x100％

圆柱和圆锥

圆柱和圆锥各部分的名称以及特征

圆柱

1.圆柱各部分的名称

1.上下两个圆面叫做底面

2.圆柱的周围叫侧面

3.两个底面之间的距离叫做高

2.圆柱的特征

圆柱的上下底面是两个圆，它们是完全相同的；圆柱的侧面是曲面；圆柱的高有无数条，且所有高的长度都相等

3.圆柱的侧面展开图是长方形（当圆柱底面周长=高时，展开后是正方形）

圆锥

1.圆锥各部分的名称

1.圆锥的底面是一个圆

2.侧面是一个曲面

3.从圆锥的顶点到底面圆心的距离是圆锥的高

4.母线：顶点到圆周上任意一点的线段

2.圆锥的特征

1.下面的一个圆面叫底面

2.他周围是侧面

3.一个圆锥只有一条高

3.圆锥的侧面沿着一条线展开后是一个扇形

基本公式

1.圆的公式

1.基本公式

1.圆的周长(C)公式：2πr=πd

2.圆的面积(S)公式：πr²

2.逆推公式

1.d=C÷π

2.r=C÷π÷2

2.圆柱/圆锥的公式

1.基本公式

圆柱

S侧：Ch=πdh=2πrh

S表：S侧+2S底=2πrh+2πr²

V柱：Sh=πr²h

圆锥

V锥：⅓πr²h

2.性质

1.圆柱和圆锥的性质

1.等底等高情况下，圆柱体积是圆锥体积的3倍（必须是等底等高才成立）

2.等底等高情况下，圆锥体积是圆柱体积的⅓（必须是等底等高才成立）

3.等底等高情况下，圆锥体积比圆柱体积少⅔（必须是等底等高才成立）

4.等底等高情况下，圆柱体积比圆锥体积多2倍（必须是等底等高才成立）

5.等体积等高的情况下，圆锥底面积是圆柱底面积的3倍（必须是等体积等高才成立）

6.等体积等底面积的情况下，圆锥的高是圆柱高的3倍（必须是等体积等底面积才成立）

3.圆柱圆锥的应用

1.圆柱的横切：切成n段，需要n-1次，增加2x（n-1）个底面积（段数-1=次数；次数x2=面数）

2.把一个正方体削成一个最大的圆柱（或圆锥），正方体的棱长就是圆柱（或圆锥）的底面直径和高

3.熔铸（或铸成），体积不变

4.注水问题

1.性质：上升的（或下降的）水的体积等于放入的物体的体积（完全浸没）

2.公式:放入物体的体积=容器的底面积x水面变化的高度

比例

1.基本性质/概念

1.比的基本性质：两个数相除，又叫做这两个数的比，“：”是比号，比号前面的数叫做比的前项，比号后面的数叫做比的后项，前项除以后项所得的商叫做比值，比的后项不能为0，比的前项和后项同时乘或除以一个相同的数（0除外），它们的比值不变

2.分数的基本性质：分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变。乘积是1的两个数互为倒数。1的倒数是1,0没有倒数

3.商不变的规律：在除法里，被除数和除数同时扩大或者缩小相同的倍数（0除外）商不变。

4.小数的性质：在小数的末尾添上0或者去掉0，小数的大小不变

5.公因数只有1的两个数叫做互质数，最简整数比就是前后两数互质

2.比例的基本性质/概念/公式

1.比例：比例是表示两个比相等的式子，比例有四个项，分别是两个外项和内向，在外面的叫做比的外项，在里面叫做比的内项，比例的四个数均不能为0

2.比例的基本性质：在一个比例中，内向之积等于外项之积

3.比例后不能带单位

3.正比例和反比例

1.解比例：根据比例的基本性质，如果已知比例中的任意三项，就可以求出比例中的另外一个未知项，所以求比例中的未知项，叫做解比例.

2.正比例

1.正比例的性质：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的的比值（也就是商）一定，这两种量就叫做成正比例的量，他们的关系叫做正比例关系。

2.用字母表示：y÷x=k（一定量）

3.正比例关系两种相关联的量的变化规律：同时扩大，缩小，比值不变。

4.判断两种量是否成正比例关系

1.先判断这两种量是不是相关联的量，一种量是不是随着另一个量的变化而变化

2.再判断这两种相关联的量中相对应的两个数的比值（也就是商）是否一定。若一定，这两种量就成正比例关系，反之就不成正比例关系

3.正比例关系图像是一条从（0,0）出发的无限延伸的射线

3.反比例

1.两种相关联的量一种量变化，另一种量也随着变化，如果这两种量中，相对应的两个数的积一定，这两种量就叫做成反比例的量，他们的关系叫做成反比例关系

2.用字母表示：xy=k（一定量）

3.反比例关系的两种相关联的量的变化规律：是一种量扩大，另一种量缩小，积不变

4.判断两种量是否成反比例关系

1.先判断这两种量是不是相关联的量，一种量是不是随着另一种量的变化而变化

2.再判断这两种相关联的量中相对应的两个数的乘积是否一定。若一定，这两种量就成反比例关系，反之就不成比反例关系

4.比例尺

1.比例尺是一幅图的图上距离与实际距离相比

2.公式为：比例尺=图上距离：实际距离

3.比例尺有两种表示方式：数值比例尺和线段比例尺，两种方式可以互换

4.比例尺的表现方式

1.数值比例尺：用数学的比例式或分数式表示比例尺的大小

2.线段比例尺：在地图上画一条线段，并标注地图上1cm所代表的实际距离

5.根据作用不同，比例尺可以分为缩小比例尺和放大比例尺

六上数学思维导图

模板简介

猜你喜欢

相关文章