高中数学选择性必修一：第三章圆锥曲线的方程_思维导图模板_知犀官网

高中数学选择性必修一：第三章圆锥曲线的方程

作者：TeacherR

0浏览2023-11-27 10:26:26

下载

使用模板已被用2次

圆锥曲线方程

3.1 椭圆

椭圆及其标准方程

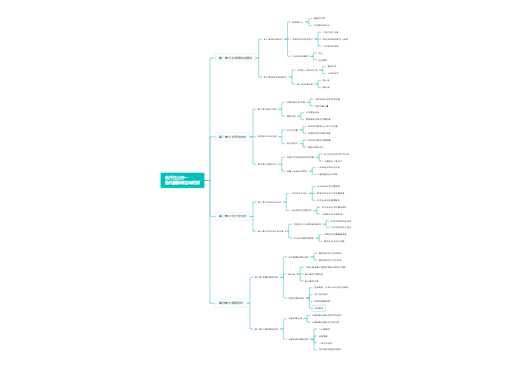
把平面内与两个定点的距离的和等于常数（大于||）的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距（2c），焦距的一般称为半焦距

椭圆标的准方程(焦点在x轴）：，其中a为动点与两个焦点的距离的和的一半（长半轴长），c为半焦距，b为（短半轴长）

椭圆标的准方程(焦点在y轴）：

椭圆的简单几何性质

范围

对称性

椭圆关于x轴、y轴对称，原点是椭圆的对称中心，椭圆的对称中心叫做椭圆的中心

顶点

椭圆与对称轴有四个交点，这四个交点叫做椭圆的顶点，线段分别叫做椭圆的长轴和短轴，它们的长分别等于2a和2b，a和b分别叫做椭圆的长半轴长和短半轴长。

离心率

椭圆的焦距与长半轴的比称为椭圆的离心率，用表示，即=，a>c>0，所以0<<1，越接近1，c越接近a，b=就越小，因此椭圆越扁平；反之，越接近0，b越接近a，这时椭圆就越接近于圆

椭圆的其他定义方式

点M与定点F的距离和M到定直线l的距离比是常数，M的轨迹是椭圆

3.2 双曲线

双曲线及其标准方程

把平面内与两个定点的距离的差的绝对值等于非零常数（小于||）的点的轨迹叫做双曲线，这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。

双曲线的标准方程（焦点在x轴上）：，其中a为动点与两个焦点的距离的差的一半（实半轴长），c为半焦距，b为（虚半轴长）

双曲线的标准方程（焦点在y轴上）：

双曲线的简单几何性质

范围

对称性

双曲线关于x轴、y轴对称，原点是椭圆的对称中心，椭圆的对称中心叫做双曲线的中心

顶点

双曲线与对称轴有两个交点，它叫做双曲线的顶点，线段叫做双曲线的实轴，它的长等于2a，a叫做双曲线的实半轴长；线段叫做双曲线的虚轴，它的长等于2b，b叫做双曲线的虚半轴长

渐近线

双曲线（a>0，b>0）的两支向外延伸时，与两条直线逐渐接近，那么这两条直线叫做双曲线的渐近线。双曲线与它的渐近线无限接近，但永不相交

当双曲线中a=b时，即实轴与虚轴等长的双曲线叫做等轴双曲线

离心率

双曲线的焦距与实轴长的比，叫做双曲线的离心率，因为c>a>0，所以双曲线的离心率>1，双曲线的离心率刻画了双曲线的“张口”大小

双曲线的其他定义方式

点M与定点F的距离和M到定直线l的距离比是常数，M的轨迹是双曲线

3.3 抛物线

抛物线及其标准方程

把平面内与一个定点F和一条定直线l（l不经过点F）的距离相等的点的轨迹叫做抛物线，点F叫做抛物线的焦点，直线l叫做抛物线的准线。

抛物线的标准方程（焦点在x轴）：，其中（，0）为抛物线焦点坐标，x=为抛物线准线

抛物线的标准方程（焦点在y轴）：

抛物线的简单几何性质

范围

p>0时，抛物线在y轴的右侧，开口方向与x轴的正方向相同；当x的值增大时，|y|的值也增大，抛物线向右上方和右下方无限延伸

对称性

抛物线关于x轴对称，把抛物线的对称轴就做抛物线的轴

顶点

抛物线和他的轴的焦点叫做抛物线的顶点，也就是原点

离心率

抛物线上的点M与焦点F的距离和点M到准线的距离d的比，叫做抛物线的离心率，用表示，=1

查看详情

模板简介

高中数学思维导图，不定期增加与更新

高中数学选择性必修一：第三章圆锥曲线的方程高中数学选择性必修一选择性必修一圆锥曲线的方程圆锥曲线

猜你喜欢

相关文章

八下历史思维导图-第五单元内容整理2022-07-20 七下历史思维导图-唐朝的兴盛思维导图2022-07-19 小数的初步认识思维导图-三年级下册数学脑图整理2022-07-18 八年级生物上册第一章思维导图：动物的主要类群2021-08-29 八年级生物上册第六单元思维导图：生物的多样性及其保护2021-08-28 八年级生物上册第五单元思维导图：生物圈中的其他生物2021-08-28 小学六年级上册数学思维导图：百分数2021-08-26 小学六年级上册数学思维导图：圆2021-08-25 小学六年级上册数学思维导图：比2021-08-24 小学六年级上册数学思维导图：分数乘法2021-08-23 小学六年级上册数学思维导图-全书2021-08-22 九年级上册政治思维导图：中国梦-初三知识点脑图整理2021-08-21 七年级上册地理思维导图：地球和地球仪2021-08-20 高中历史必修一思维导图：现代中国的政治建设与祖国统一2021-08-19 高中历史必修三思维导图：中国近代前期思想变化2021-08-18 高中历史必修二思维导图：中国近代前期政治2021-08-17

您的想法与建议，对知犀思维导图的优化改进非常有用！欢迎反馈！