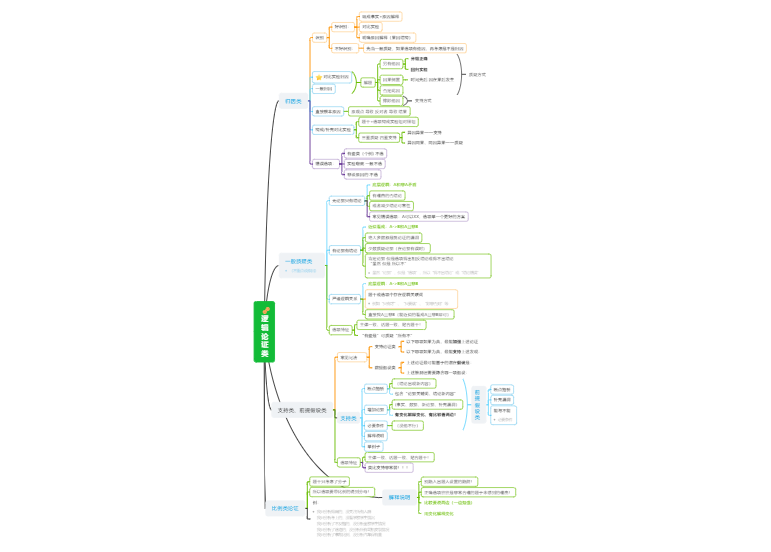
▶ 基期、末期(前期、本期)
基期,表示的是在比较两个时期的变化时,用来做比较值(基准值)的时期,该时期的数值通常作为计算过程中的除数或者减数:
末期,相对于基期而言,是当前所处的时期,该时期的数值通常作为计算过程中的被除数或者被减数。
※【注】与谁相比,谁为基期。
▶ 增长量、增长率(增长速度、增长幅度)
增长量,表示的是本期与基期之间的绝对差值,是一绝对量。
增长率,表示的是本期与基期之间的相对差异,是一相对量。
在一般情况下,“增长率”等价于“增长速度(增速)”等价于“增长幅度(增幅)”。
▶ 同比、环比
同比,指的是本期发展水平与历史同期的发展水平的变化情况,其基期对应的是历史同期。
环比,指的是本期发展水平与上个统计周期的发展水平的变化情况,其基期对应的是上个统计周期。
▶ 百分数、百分点
百分数,表示的是将相比较的基期的数值抽象为 100,然后计算出来的数值,用“%”表示,一般通过数值相除得到,在资料分析题目中通常用在以下情况:
(1)部分在整体中所占的比重:
(2)表示某个指标的增长率。
百分点,表示的是增长率、比例等以百分数表示的指标的变化情况,一般通过百分数相减得到,在资料分析题目中通常用在两个增长率、比例等以百分数表示的数值的差值这样的情况。
▶ 倍数、翻番、成数
倍数,指将对比的基数抽象为 1,从而计算出的数值。
翻番,指数量的加倍,翻一番即变成原来的 2 倍。所用的公式为:
本期/基期= 2^n,即翻了 n 番。
成数,一成为总量的 10%,二成为总量的 20%,以此类推。
需要注意的是:“A 是 B 的多少倍”和“A 比 B 多多少倍”之间的关系。
▶ 比重、比值、平均
比重(单位相同):某事物在整体中所占的分量,计算公式为“比重 =
部分/整体× 100%”。整体中各部分的比重和为 100%,若整体由 A、B 两部分组成,则 A 提升的比重等于 B 下降的比重。若题目中出现“占”字时,考察
的即是比重问题。
比值:两数相比所得的数值。
平均(单位不同):将总量分成若干份,“均”字之前、“每/平均每”字之后的量做分母,可记为“均前每后做分母”。
▶ 进出口相关问题
该类问题需要谨慎识别所问问题是进口、出口还是进出口相关:是“额”(单位一般为元、美元)还是“量”(单位一般为万吨、亿吨)。
顺差、逆差:贸易出口额大于进口额为贸易顺差、反之为逆差。
▶ 三大产业和产业增加值
产业增加值:该行业在周期内(一般以年计)比上个清算周期的增长值。该描述为固有名词,为本期量,切忌与增长量混淆。
国内生产总值(GDP)为三大产业增加值之和。
五年计划:
2006-2010 年,称之为“十一五计划”:
2011-2015 年,称之为“十二五计划”:
2016-2020 年,称之为“十三五计划”:
2021—2025 年,称之为“十四五计划”。
▶ 名义增长率和实际增长率
名义增长率未扣除价格因素,实际增长率为扣除价格因素。
计算公式:名义增长率=实际增长率+通货膨胀率。
示例
▶ 人口自然增长率
人口自然增长率简称“自然增长率”。一定时期内(通常为一年)人口自然增加数(出生人数减去死亡人数)与同期平均总人口数之比,用千分数表示。
▶ 货物周转量
货物周转量是运输企业所运货物吨数与其运送距离的乘积,以复合指标吨公里或吨海里为单位表示。
货物周转量=货物运输量×运输距离。
PS:货物周转量可以根据单位记忆,其单位为“吨公里”,即“吨”与“公里”的乘积。
文字材料具体顺序:
看资料首句,确定材料时间——从问题入手——分析问题(重中之重)——选取关键字——回到原文寻找关键字所在语段——圈出所给数据——根据问题进行分析计算。
挑选关键词原则:简略、特别(英文缩写,带有“”等等)。
图表类/综合类题目,需先阅读图表标题,圈出重点词。
ABRX四量关系:A=前期,B=本期,X=变化量,R=变化率。[B=A+X, X=AR]
关于上述四量的问题,均是给出两量作为已知量去求得另外两量,同学应该把四量间的本质关系牢记于心。
在多个数字精确求和时,从细节处入手,在各个选项中选出正确答案。观察选项,在倒数第几位出现完全不同,就观察末位几位。
※【注】尾数法也非常适用于精确求差。
和我们记忆中的列竖式做加法顺序正相反,高位叠加是从高位加起,抓住问题的主要矛盾。非精确求和或没有选项可以参考时,可以选用高位叠加法。
若几个相近数字求和,可以先找出基准值,再根据“偏离总和”求得总和或平均值。
被减数-减数=(被减数-基准值)+(基准值-减数):
例如“632-589”,我们可以加入 600 作为基准值,则 632-589=(632-600)+(600-589)。
将三位数的减法分成“21”或“12”两段,尽可能保证不用借位。
若乘法中有某个乘数可以近似的转化为某个常见分数,我们可以将多位数乘法转化为简单除法计算。
拆分法的本质是将被除数由大到小拆成几部分分别计算,通过逐步分解,从而得出结果。【拆分法使用规则】
方法练习
拓展:乘法拆分
若乘法中有某个乘数为百分数且能拆成两个简单数值(50%、10%、5%等),我们可以将该百分数拆成两部分再相乘。
常用的小数拆分如下:45%=50%-5%:55%=50%+5%:15%=10%+5%:60%=50%+10%:95%=1-5%:90%=1-10%,所有 50%、100%附近数等。
方法拓展之分子分母同时拆分(盐水思想运用)
分子分母同时拆分可判断分数大于或小于某一个数值,在综合分析题目中最适用,使用前提有二:
一是分数的分子分母可以分别简单的拆分成两部分,且满足一大杯和一小勺的关系(即一部分所占比重极大,起主导作用,另一部分比重极小,只起到调节作用):
二是拆出的一大部分容易计算,否则没有必要使用此方法。
【即在实际列式过程中,左侧大部分起决定性作用,右侧小部分起调节性作用。】
一般来讲,在本期 B 和增长率 R 是已知量的前提下,我们可以用 415 份数法求得基期 A、变化量 X 的数值。
415 份数法中“415”分别代表基期、变化量、本期的份数,一般来说,我们只需根据增长率求出本期对应的份数,即可根据本期量求得一份的大小,再根据问题进行下一步计算。
例如:若增长率为 25%(25%=1/4),为方便计算我们可以将基期设为 4 份,变化量 X=AR=1 份,本期为基期和变化量的和,即为 5 份。则基期、变化量、本期的份数分别为 4、1、5。这也是 415 份数法名字的由来。
二、415 份数法使用步骤
①将增长率 R(百分数)化成相近的分数 a/b:
②写出或在头脑中想出基期、变化量、本期量之比 b:a:a+b(基期为 b 份,变化量为 a 份,本期为 b+a 份):
③根据本期实际量和其对应的份数求得一份量:
④根据一份量的大小和变化量、基期对应的份数继续求解。
一、分配法使用的核心公式为 X=AR。
二、假设分配法使用时机
①在增长率很小(一般认为小于 10%)或增长率不在任何分数附近时,求前期或变化量可以使用分配法:
②能初步判断出前期靠近一个整数(5000、10000 等)时,可使用假设分配法:
三、假设分配法使用步骤
①确定被分配数和增长率:
②画出分配树,逐步确定所求量(前期 A、变化量 X):
③尽量将前期分成整数,方便计算:
④最后一步可直接根据 X=BR 确定 X 值,误差完全可以忽略。
【注】若增长率为负,假设分配法较繁琐,不十分适用。
考法:① 直接求增长量X;② 求两个增长量X的关系(或背书、比值等)。
求 X 的类型题一般会给出 B、R 做已知条件,我们可以根据 R 的大小选择适用的方法:
当 R 大于 10%并靠近某个分数时,可以选用 415 份数法:
当 R 小于 10%时,可以选用假设分配法(用熟悉之后就是万能的):
当 R 非常小(一般为小于 5%),并且选项的差距很大,我们可以用 B×R 代替 A×R 来求得 X。
一、增长率的四种常见考察方式
一是基本增长率(最基本的考法):已知条件为本期和基期求 R,可用 R = X/A 求解:
二是隔年增长率:已知条件为两年的增长率 R1、R2,求两年增长率 R,可用 R=R1+R2+R1R2求解(例如,14年增长率为 R1,13 年增长率为 R2,则 14 年较 12 年增长率为 R1+R2+R1R2):
三是比值增长率:增长率指的是本期比前期增长的情况,但如果本期和前期均为一个比值(A、B),此类增长率即为比值的增长率问题:
四是乘积增长率,如 A=B×C,已知 B、C 增长率,要求 A 的增长率,Ra=Rb+Rc+Rb×Rc(与隔年增长率相同)。
三、比值增长率的特殊说明
比值的增长率,本质上考察的仍然是增长率,和 R 的前两种考法不同的是,所求的是“比值”而非“数值”的增长率。
五、乘积增长率的特殊说明
乘积增长率,顾名思义,即两个乘数之积的增长率,其公式与隔年增长率一。
一、最常见考法与思路
一是最基本的考法,直接求前期 A,我们可以根据 R 的大小和选项的差距选择不同的解题方法:若选项相距很近,我们可以选择直除法:若选项有一定差距,我们可以选择直接代入法、415 份数法:
二是求隔年前期,可先求出隔年增长率,即变成第一类考法:
三是前期差值,即需要我们求出两个前期再做差:此类题目求前期时没有选项参考,计算量较大,性价比一般,我们可以先用追及思想粗略判断前期差值的情况,排除不符合选项:若无法秒杀,我们可选用 415 份数法、假设分配法、直除法依次求得两个前期。
一、题型介绍
此类题型(求 B)考察次数极少,也相对简单,一般只需要套用公式 B=A+AR 或 B=A(1+R)^n即可,但有
因将来未发生的情况无法判断,所以此类题目一般会让我们根据某一假设的增长率来计算。
※【注】B=A×(1+R)^n为年均增长率公式。
① 直接计算某一部分的本期比重。
所用公式:比重=部分/整体:部分=整体×比重:整体=部分/比重
② 多部分本期比重,或求部分和或部分差。
所用公式:部分和(部分差)=整体×比重和(比重差):
比重和(比重差)=部分和(部分差)/整体
需要注意的是,前期平均值、前期倍数、前期比值均可看作是特殊的“前期比重”,利用前期比重公式进行计算。
隔级比重,指的是题目中存在大集合、中集合、小集合的关系,所问的是小集合和大集合之间的情况。
例如,学校为大集合,班级为中集合,班级内的女同学为小集合,若问的是班级内的女同学在学校中的比重为为多少,即是隔级比重。
与前期比重一样,平均值、倍数、比值也可看作是特殊的“比重问题”,均可利用比重趋势判断方法判断变化情况。
比重差与比重趋势在本质上是一类考法,指的都是两期比重的变化情况。区别在于比重趋势是定性的分析比重的变化(变大或变小),比重差是定量的分析比重变化(变大多少或变小多少)。
多数题目可简单根据比例关系确定答案,注意 1/2、1/4、1/6 等:而且画图存在规律,一般是从 12点钟开始,按照顺时政方向依次排列。
资料分析题目中,经常会有整体(增长率),部分 A(增长率),部分 B(增长率)的关系,这样的关系和混合溶液(浓度),溶液 A(浓度),溶液 B(浓度)的关系非常相似,所以,我们可以将盐水思想和十字相乘法运用到资料分析中。
但需要注意的是,资料分析中的增长率 R,是针对前期 A 所言,X=A×R,所以如果要用十字交叉法求解,溶液 A、B 质量对应的是前期值。
题型分析:求人数,想盐水
题型分析:盐水类之两部分之比
题型分析:盐水问题之时间分段
十字交叉法介绍
定性分析法
双线法介绍
第一句:B 越大 R 越大则 X 越大:
第二句:我的 B 是你的 N 倍,你的 R 是我的 N 倍 以上,我们的 X 才可能相等。
一是注意起始、结束年份、月份(重中之重):
二是注意“合计”“总计”行,以免数错:
三是注意第一年的增量:
四是注意单位(例如航空运输)。
均前每后(平均每也是每)是分母,时间平均值注意起止时间(11 个月)和平闰年、A/B/C/D=AD/BC.
1.注意时间!求哪几个月的平均数一定要看清楚!
2.均前每后做分母(后除以前)
3.普通闰年:公历年份是 4 的倍数,且不是 100 的倍数的,为闰年(如 2004 年、2020 年等就是闰年)
世纪闰年:公历年份是整百数的,必须是 400 的倍数才是
闰年(如 2100 年不是闰年,2000 年是闰年)。
·若占比和超过 100%,则一定有交集:
·若问至多,则考虑“包含”,至多有“较少比重”:
·若问至少,则考虑尽量“相斥”,套用公式:“a + b − 100%”或“a + b-总量”。