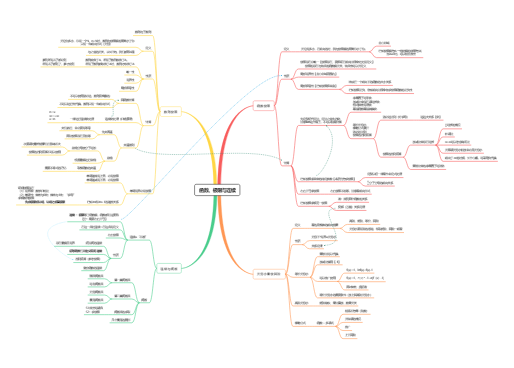
原函数
不定积分
连续函数一定有原函数
区间上有第一类间断点,在该区间没有原函数
存在第二类间断点,可能有,可能无
不定积分的性质
基本积分公式
第一类换元法(凑微分法)
第二类换元法
分部积分法
有理函数积分
①万能代换(一般法)
②三角变形,换元,分部(特殊法)
令根号下的一堆=t
定义
1)比较判别法
2)比较法的极限形式
3)P积分
定义
1)比较判别法
2)比较法的极限形式
3)P积分
直角坐标系
极坐标系
二重积分、元素
横截面面积的体积
常用曲线:
双纽线
摆线
星形线
心形线(数三)
常见函数
边际函数、边际分析
注意需求价格弹性的正负!
分匀合精
一重:线与坐标轴围成的面积
二重:线与线围成的面积
有正负
函数在[a,b]连续,积分存在
在[a,b]有界,且只有有限个间断点,积分存在
在[a,b]上只有有限个第一类间断点,积分存在
积分存在,函数在[a,b]有界
牛顿莱布尼茨公式
换元积分
分部积分
利用奇偶性、周期性
点火公式
∫(0,π)xf(sinx)dx=π/2∫(0,π)f(sinx)dx
变上限积分
不等式
积分中值定理、广义积分中值定理
计算不定积分
不定积分杂例
多做,积累题型
概念、性质、存在准则
连乘形式:①夹逼②取对数
也有不等式和积分中值定理的使用
先考虑下奇偶性,但有些题可能直接做更简便
总结计算方法
连续性:f(x)在[a,b]可积,则变上限积分在[a,b]连续
可导性:变上限积分在区间除x0点外均连续,则在x0处①连续②可去③跳跃的可导性及值
理解!!记住!P112
奇偶性:第一章函数奇偶性
处理变上限积分常用:洛必达、等价无穷小代换、积分中值定理
定积分不等式性质
变量代换
积分中值定理
可以将f(x)与其导数联系起来
柯西积分不等式
1)比较判别法
2)比较法的极限形式
3)P积分
核心用法:换元、分部
要积累!
先画草图!
经济学中的应用
关联