物理化学第一章热力学第一定律_思维导图模板

热力学第一定律

热力学概论

热力学研究的基本内容

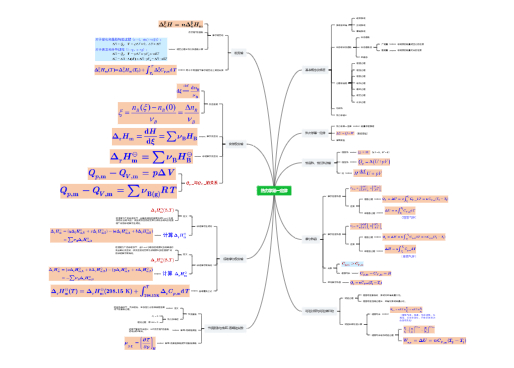
研究热、功和其他形式能量之间的相互转换及其转换过程中所遵循的规律

研究各种物理变化和化学变化过程中所发生的能量效应

研究化学变化的方向和限度

化学热力学研究的内容

热力学第一定律---计算化学变化中的热效应

热力学第二定律---计算变化的方向和限度，特别是化学反应的可能性以及平衡条件的预示

热力学第三定律---物质的熵的绝对值定律，解决化学平衡中的计算

热力学的方法和局限性

热力学方法

研究对象是大数量分子的集合体，研究宏观性质，所得结论具有统计意义

只考虑变化前后的净结果，不考虑物质的微观结构和反应机理

能判断变化能否发生以及进行到什么程度，但不考虑变化所需要的时间

局限性

不知道反应的机理、速率和微观性质，只讲可能性，不讲现实性

热力学基本概念

系统与环境

敞开系统

系统与环境之间既有物质交换，又有能量交换。

封闭系统

系统与环境之间无物质交换，但有能量交换。

孤立系统

系统与环境之间既无物质交换，又无能量交换。

系统的性质

广度性质

具有加和性

强度性质

不具有加和性

热力学平衡态

热平衡

系统各部分温度相等

力学平衡

系统各部的压力都相等，边界不再移动

相平衡

多相共存时，各相的组成和数量不随时间而改变

化学平衡

反应系统中各物质的组成不再随时间而改变

始态：系统变化前的状态；终态：系统变化后的状态

状态函数与状态方程

系统的状态是系统一切性质的综合表现

状态函数

定义

由系统状态确定的系统的各种热力学性质，称为系统的状态函数

特点

状态函数是状态的单值函数

状态函数的改变量只取决于系统始、终态，与变化的途径无关

异途同归，值变相等；周而复始，值变为零

状态函数的微小变化，在数学上是全微分

不同状态函数构成的初等函数（和、差、积、商）也是状态函数

异途同归，值变相等；周而复始，数值还原

状态方程

系统状态函数之间的定量关系式称为状态方程

对于一定量的单组分均匀系统，状态函数 p, V，T 之间有一定量的联系。经验证明，只有两个是独立的，它们的函数关系可表示为：
T=f(p,V) P=f(T,V) V=f(T,P)

过程与途径

过程

等温过程

等压过程

等容过程

dV=0

绝热过程

Q=0

循环过程

途径

完成某一状态变化所经历的具体步骤称为途径。由同一始态到同一终态的不同方式称为不同的途径

热和功

热

系统与环境之间因温差而传递的能量称为热，用符号Q 表示

系统吸热，Q>0；系统放热，Q<0

功

系统与环境之间传递的除热以外的其它能量都称为功，用符号W表示

系统对环境作功，W<0；环境对系统作功，W>0

在化学热力学中，将功分为两种，即体积功（W）和非体积功（W）；经常遇到的是体积功

Q和W的单位都用能量单位焦耳 “J” 表示

Q和W都不是状态函数，其数值与变化途径有关

Q和W的微小变化用符号而不能用表示

热力学第一定律

第一定律的表述方式

热力学第一定律就是能量守恒定律

不供给能量而连续不断做功的第一类永动机是不可能造成的

自然界的一切物质都具有能量,能量有多种不同的形式,能量可以从一种形式转化为另一种形式,能量的总量在转化过程中保持不变

热力学能

系统总能量构成

系统整体运动的动能

系统在外力场中的位能

热力学能，也称为内能

热力学中一般只考虑静止的系统，无整体运动，不考虑外力场的作用，所以只注意热力学能

热力学能，亦称为内能，它是指系统内部能量的总和，热力学能用符号U表示，

热力学能的绝对值尚无法确定，只能求出它的变化值

热力学能是系统的性质，是状态函数。也是系统的广度性质

内能是温度体积（或压力）及物质的量的函数

数学表达式

封闭系统，从状态1变为状态2，若系统从环境吸收了Q的热，系统对环境作了W的功。根据热力学第一定律，此系统热力学能的改变ΔU为：
ΔU = U2 - U1 = Q +W

若系统所发生的变化非常微小，则：
d U = δQ +δW

可逆过程与体积功

体积功

pe = 外压
A= 截面积
dl = 活塞移动距离
dV = Adl = 体积的变化
δW = -F dl = -pe Adl
δW = -pedV

对于宏观过程

功与过程

设在定温下，一定量理想气体在活塞筒中克服外压，经4种不同途径，体积从V1膨胀到V2所作的功

自由膨胀

恒外压膨胀（pe保持不变）

多次定外压膨胀——三次膨胀

准静态膨胀过程

显然 W4 > W3 > W2 > W1
使系统内压与外压处于无限接近的情况下，即膨胀次数无限多，
系统自始至终是对抗最大的阻力情况下，所此过程所作的功为最大功。这种过程又称为准静态过程。

若采取与以上过程相反的步骤，将膨胀后的气体压缩到初始的状态

恒定外压p1下压缩过程

多次恒外压压缩过程

准静态压缩过程

功与变化的途径有关

准静态膨胀，系统对环境作最大功；准静态压缩，环境对系统作最小功

可逆过程

体系经过某一过程从状态（1）变到状态（2）之后，如果能使体系和环境都恢复到原来的状态而未留下任何永久性的变化，则该过程称为热力学可逆过程。

不可逆过程

体系经过某一过程之后，如果用任何方法都不能使体系和环境完全复原，则该过程称为热力学不可逆过程。

可逆过程的特点

可逆过程是以无限小的变化进行，体系始终无限接近于平衡态

体系在可逆过程中作最大功，环境在可逆过程中作最小功，即可逆过程效率最高

沿与过程原来途径相反方向进行，可使体系和环境完全恢复原态

焓

等容反应热

封闭系统在非体积功为零，等容

恒容过程，体积功为零

在非体积功为零的条件下，封闭系统经一等容过程，所吸收的热全部用于增加系统的热力学能。

Qv只取决于系统的始态和终态

W，=0,恒容，式中QV为恒容过程的热效应

等压反应热

封闭系统，非体积功为零且恒压（p1=p2=pe）

Qp为恒压过程的热效应

焓

热力学上定义为焓（enthalpy），用H 表示

W，=0,恒压

焓是状态函数, 只取决于系统的始、终态

不能确定焓的绝对值，但可求变化值

焓也是广度性质，并具能量的量纲

在非体积功为零的条件下，封闭系统经一等压过程，所吸收的热全部用于增加系统的焓

热容

热熔的概念

对于不发生相变和化学变化的均相封闭系统，非体积功为零，热容的定义是：
系统升高单位热力学温度时所吸收的热

常用的热容

比热容

规定物质的数量为1 g（或1 kg）的热容

摩尔热容Cm

规定物质的数量为1 mol的热容

恒容热容

封闭系统恒容过程的热容称为恒容热容

无化学变化和相变化且非体积功为零的封闭系统

恒压热容

在非体积功为零的恒压过程中，恒压热容Cp可表示为：

dH=CpdT

无化学变化和相变化且非体积功为零的封闭系统

热容与温度的关系

热力学第一定律的应用

理想气体

热力学能和焓

焦耳实验

结论：理想气体的热力学能 U只随T而变

解释：理想气体分子之间无作用力，无分子间位能，体积改变不影响热力学能

理想气体的热力学能和焓仅是温度的函数

理想气体的Cp、CV也仅是温度的函数

理想气体的Cp、CV之差

对于没有相变化和化学变化且只作体积功的封闭体系，其CP与CV之差为

即理想气体的Cp.m与 CV.m均相差一摩尔气体常数R 值

理想气体的绝热过程

理想气体在W′=0条件下的绝热可逆过程中的方程式

绝热过程的功

定组成封闭系统理想气体的一般绝热过程，不一定是可逆过程

W=CV (T2－T1)=nCV,m (T2－T1)

绝热可逆与定温可逆过程的比较

因为绝热过程靠消耗热力学能作功，要达到相同终态体积，温度和压力必定比B点低

热力学第一定律应用于实际气体

节流膨胀

这种维持一定的压力差的绝热膨胀称为节流膨胀。当节流膨胀经过一定时间达到稳定状态后，左、右侧气体的温度稳定不变，实测值分别为T1与T2，且T1≠T2

节流膨胀是恒焓过程

因为Q=0，所以ΔU = W

环境对系统作功： W1= -p1ΔV ＝ p1 V1

系统对环境作功：W2= -p2ΔV =-p2V2

焦耳-汤姆逊系数

实际气体的焓不仅取决于温度，而且与气体的压力有关

假设节流膨胀在dp的压差下进行，温度的改变为dT

μJ-T 的大小，既取决于气体的种类，又与气体所处的温度、压力有关

热化学

化学反应的热效应

热效应

在非体功为零的条件下，封闭系统中发生某化学反应，当产物的温度与反应物的温度相同时，体系所吸收或放出的热量，称为该化学反应的热效应

系统吸热，热效应为正

系统放热，热效应为负

恒容热效应与恒压热效应

理想气体

反应进度

对反应物取负值，对生成物取正值

反应进度

引入反应进度的最大优点是，不论反应进行到任何时刻，用任一反应物或产物所表示的反应进度都是相等的

反应进度为1mol时引起体系的焓变和内能变化分别称为摩尔反应焓变（ΔrHm）和摩尔反应内能变化（ΔrUm ）

ΔrHm和ΔrUm分别表示的是按所给化学计量方程式完成一个单位化学反应所产生的焓变和内能变化，其值取决于化学计量方程式的具体形式

热化学方程式

同时表明热效应ΔrHm和ΔrUm值及物质状态的化学反应方程式称为热化学方程式

写出该反应的计量方式

因为U，H 的数值与体系的状态有关，所以方程式中应该注明物态、温度、压力、组成等。对于固态还应注明结晶状态

用△rHm表示反应的摩尔等压热效应，应标明反应时的温度△rHm(T)

在化学反应计量方程式后空格或加分号，然后写下△rHm以及数值与单位

当物质的状态，反应方程式进行的方向和化学计量数等不同时，热效应的数值和符号也不相同，即必须与所给反应的计量方程相对应

化学反应热效应的计算

赫斯定律

反应的热效应只与起始和终了状态有关，与变化途径无关。不管反应是一步完成的，还是分几步完成的，其热效应相同

实验表明，赫斯定律只是对非体积功为零的等容反应和等压反应才严格成立

由标准的摩尔生成焓计算ΔrHm

等温等压下化学反应的热效应等于生成物焓的总和减去反应物焓的总和

人为规定：在标准压力Pθ（100kPa）和指定温度T时，由最稳定的单质合成标准状态下1摩尔化合物的焓变称为该化合物在此温度下的标准摩尔生成焓

式中pB和rB分别表示产物和反应物在化学计量方程式中的计量系数。系数B对反应物为负，对产物为正

由标准的摩尔燃烧焓计算ΔrHm

在标准压力P =100KPa和指定温度T下，1摩尔物质完全燃烧的等压热效应称为该物质的标准摩尔燃烧焓

所谓完全燃烧是指被燃物质变成最稳定的氧化物或单质（即最稳定的产物）

由键焓估算ΔrHm

键能—断裂气态化合物中的某个具体的键生成气态原子所需的能量称为键的分解能即键能，可以用光谱方法测定

键焓—诸种化合物中该键能的平均值
在双原子分子中，键焓与键能数值相等

一个化学反应的热效应等于反应物的总键焓减去产物的总键焓

实际上, 只要考虑起变化的化学键的键焓

用键焓估算是不够精确的，只是作出初步的估算的方法

由离子标准摩尔生成焓计算ΔrHm

因为溶液是电中性的，正、负离子总是同时存在，不可能得到单一离子的生成焓

规定：标准压力下，在无限稀释的水溶液中，H+的摩尔生成焓等于零

其它离子生成焓都是与这个标准比较的相对值

aq表示水溶液，∞表示为无限稀释的溶液

溶解热和稀释热

溶解热

在等温等压下，一定量的物质溶于一定量的溶剂中所产生的热效应称为溶解热，它是破坏晶格的晶格能、电离能和溶剂化热效应的总和

摩尔积分溶解热

在等温等压且非体积功为零的条件下，将nB摩尔的溶质B溶于一定量的溶剂中形成一定浓度的溶液，若整个过程的焓变为，则摩尔积分热定义为

即为1摩尔溶质形成一定浓度溶液的溶解热。其大小与溶质、溶剂的种类、与温度、压力及所形成的溶液的浓度有关

摩尔微分溶解热

在恒温恒压且非体积功为零的条件下，在一定浓度的溶液中，再加入dnB摩尔的的溶质B，产生的微量热效应为dH，则该溶质在该浓度的微分摩尔溶解热定义为

摩尔微分溶解热不能用量热法测定，可测定不同数量的溶质在一定量溶剂中的积分溶解热，再做图，曲线上某点的斜率即为该浓度的摩尔微分溶解热

稀释热

积分稀释热

在恒温恒压下，将一定量的溶剂加到一定浓度的溶液中，使之稀释成另一浓度的溶液时所产生的热效应称为积分稀释热。用ΔidilH表示

积分稀释热的值可以从积分溶解热求得。（浓度1→浓度2）

微分稀释热

在等温等压及一定浓度的溶液中，再加入dnA摩尔的溶剂产生δQ的热效应,则摩尔微分稀释热的定义为

它的值无法直接测定，从微分溶解热曲线上作切线求得

不同温度的ΔrHm——基尔霍夫定律

在等压条件下，若已知下列反应在T1时的反应热效应为△rHm(T1)，则该反应在T2时的热效应△rHm(T2)，可用下述方法求得

若 ,△Cp=0则反应热不随温度而变；若,△Cp>0则当温度升高时，反应热将增大；
若,△Cp<0则当温度升高时，反应热将减小

若温度变化范围不大时，可将△Cp视为常数，则式（1）可写成

若反应物和产物的恒压热容与温度有关

若在T1-T2范围内，反应物或产物有相变化
由于Cp,m 与T 的关系是不连续的，因而必须在相变化前后进行分段积分，并加上相变潜热

物理化学第一章热力学第一定律

模板简介

猜你喜欢

相关文章