高等数学第一章函数极限连续_思维导图模板

函数极限连续

第一节函数

函数的概念及表示

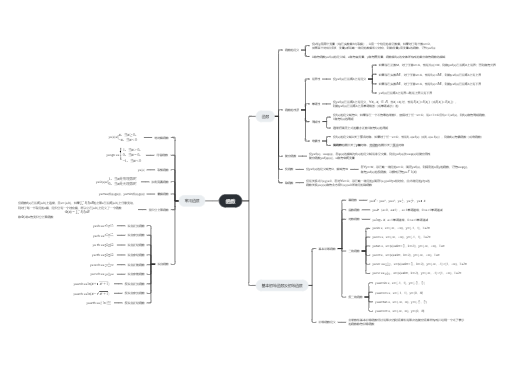
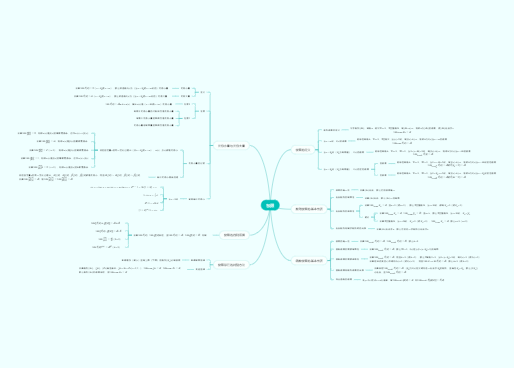
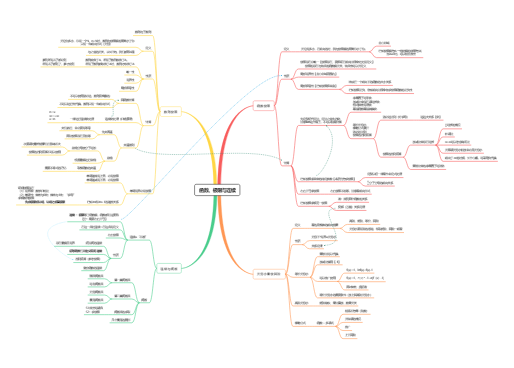
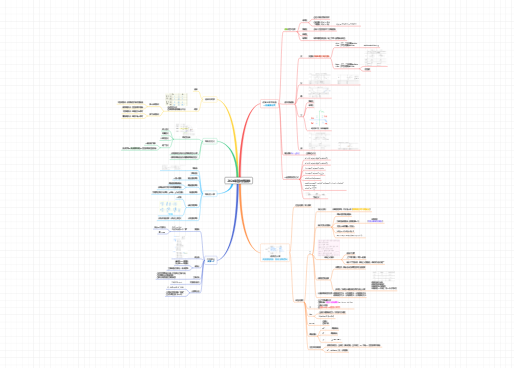
1、函数的概念
①一个或多个变量X对应一个确定的数值Y；
②决定函数的两个基本要素：定义域和对应规则；

函数的定义域要注意的原则：

函数的性质

单调性

①利用单调性的定义求函数的单调性；

②利用一阶导数的正负判断函数的单调性；

奇偶性

①函数的定义域关于原点对称；
②满足 —偶函数 —奇函数；
③奇函数关于原点对称，偶函数关于y轴对称；

①根据奇偶性的定义判断函数的奇偶性；

②根据函数奇偶性的运算性质判断奇偶性；

周期性

①根据周期性的定义判断函数的周期性；

②根据函数周期性的运算性质判断周期性；

有界性

定义：有界函数 |f(x)|≤M 无界函数 |f()|＞M

①根据有界性的定义判断函数的有界性；

初等函数

初等函数：由常数和基本初等函数经过有限次四则运算和有限次的函数复合所构成并可以用一个式子表示的函数。

基本初等函数
的性质及其图形

幂函数

指数函数

对数函数

①对数函数和指数函数互为反函数；

三角函数

正弦函数和余弦函数
①奇偶性相反；

正弦函数

余弦函数

正切函数和余切函数
①记住函数的定义域；
②奇偶性相同（奇函数）；
③以π为周期；

正切函数

余切函数

正割函数和余割函数
①奇偶性相反；
②记住关系式；

正割函数

余割函数

反三角函数

反正弦函数与反余弦函数
①具有了单调性，反正弦函数单调增，反余弦函数单调减；
②奇偶性：只有反正弦函数具备奇偶性（奇函数）；
③

反正弦函数

反余弦函数

反正切函数和反余切函数
①具有了单调性；
②只有反正切函数有奇偶性；
③

反正切函数

反余切函数

特殊函数

分段函数

分段函数：是指对其定义域内的自变量的不同取值，与其相对应的法则也不同；需要用到两个或两个以上的数学表达式来表示。（如：有绝对值符号的函数）

复合函数

1.内侧函数的值域与外侧函数定义域相交不为空集；
2.复合函数的定义域满足：
①X满足内侧函数的定义域；
②内侧函数的值域满足外侧函数的定义域。

①结合分段函数，求复合函数的定义域和表达式；
首先要根据“复合函数的定义域”的性质，确定其X的定义域；
然后将内侧函数代入，解得复合函数的表达式。

②已知复合函数的表达式，求其外侧函数的表达式；
将内侧函数换元，将X的函数换算为单个函数变量 t。

③已知复合函数和外侧函数的表达式，求内侧函数的表达式；
将外侧函数的X换算成内侧函数，就会等于复合函数的表达式，从而求解出内测函数的表达式。

反函数

①函数和反函数的定义域和值域相互对换；
②反函数要求函数要满足：一个 X 对应一个 Y ;
③单调函数（满足第二条）一定有反函数，反之则不然；
④函数：反函数：

①根据函数与反函数的基本表达式求反函数；

隐函数

如果方程f(x,y)=0能确定y是x的函数，即E与Y在等式的同一侧；那么称这种方式表示的函数是隐函数。

①利用隐函数的求导法则求隐函数的导数；
对方程两边分别求导，换算得出隐函数的倒数函数，再代入X的取值。

函数关系的建立

在建立函数关系时,首先要确定问题中的自变量与因变量,再根据它们之间的关系列出等式,得出函数关系式,然后确定函数定义域,确定定义域时,不仅要考虑到函数关系的解析式,还要考虑到变量在实际问题中的含义。

第二节极限

数列极限的
定义与性质

①可以理解为：存在一个值 a，当数列趋向于无穷时，数列的极限值与数值 a的接近程度趋近于 ε ；
②如果一个数列有极限，也成该数列收敛，否则就称发散。

记住以上结论：

①利用数列极限的充分必要条件求函数的极限；
利用数列极限的推论证明极限的存在；

②利用数列极限的定义证明极限成立；

函数极限的
定义与性质

①自变量区域无穷大时函数的极限；
②自变量趋于有限值时函数的极限；

①利用极限的充分必要条件判断极限是否存在；

②分段函数求极限；
应该先求出分段点，再求分段点的左右极限；最后根据分段点左右极限是否存在且相等，判断函数的极限。【若表达式中含有】

记住以上两种特殊的函数形式

记住以上结论（函数的左极限和右极限）：

函数的性质

有界性

①如果数列收敛，那么数列一定有界，但反之不成立；
【收敛与有界的区别：收敛函数在定义域的每一点都收敛，指会聚于一点，向某一值靠近；有界函数则是指函数有最大值和最小值，如果定义域内存在不存在的一点，那么此时函数依旧有界，但是不收敛。】
②若自变量趋于有限值的函数极限存在，那么该函数在有限值的某去心领域内有界（即局部有界）；但反之不成立。

①判断函数在指定定义域内是否有界；
求函数在指定定义域内的极限。

②求函数在哪个区间内有界；
利用函数极限的局部有界性质，满足该函数在定义域区间内连续，求函数在区间端点的极限是否存在；如果左右极限都存在，那么函数就在该区间内有界。

保号性

函数极限的保号性是指满足一定条件（例如极限存在或连续）的函数在局部范围内函数值的符号保持恒正或恒负的性质。
通俗的说：对于函数f(x)，当x趋向于0时，函数是正数，那么在0的周围范围内该函数的值还是正数。注意理解这个周围，这个周围是指0的左右两边，如果题目极限说趋向于0+，那么周围指的就是从正数趋向于0的那部分。

函数极限与数列极限的关系（海因定理）

无穷的概念

无穷小

无穷小：是指当函数趋于无穷或有限值时，函数的极限值为0。

①根据无穷小的性质求函数的极限；

②求函数间的无穷小关系；

③根据无穷小的等价无穷小替换求函数的极限；

④利用极限值与无穷小之间的关系求函数的极限；

无穷小的性质

①有限个无穷小的和、积仍是无穷小；
②无穷小量与有界量的积仍是无穷小。

无穷小的比较

无穷大

无穷大：是指当函数趋于无穷或有限值时，函数的极限值为 ∞。
①无穷大量必为无界变量，而无界变量不一定是无穷大量；
②无穷大的性质：两个无穷大的积仍是无穷大量；
无穷大量与有界变量之和仍是无穷大；
无穷大量与非零常数乘积仍是无穷大量。

①利用无穷大的性质求函数的极限；

②利用无穷大量常用比较求解；

无穷大量与无穷小量的关系

求极限的重要方法

1、极限的四则运算

①利用四则运算法则、常用极限结论求极限；

常用的结论（记住）

2、两个重要的极限

第一重要极限

第二重要极限

3、等价无穷小替换原则

①对分子或分母中的一个或几个无穷小因子作等价替换；

和差关系在满足一定条件下可以作等价替换（可作结论用）。

4、洛必达法则

极限存在的两个标准

5、单调有界准则

单调有界数列必有极限，
单调递增有上界必有极限，单调递减有下界必有极限。
①证明数列单调有界（多用数学归纳法）；
②对给定的关系式两边求极限，解出 a 。

6、夹逼准则

①放大缩小建立不等式；
②验证不等式两头的极限存在且相等；

7、利用函数的连续性求极限

8、利用泰勒公式求极限

第三节连续

函数连续的概念

①定义一：在某一点周围趋近于0的范围内，Y值的距离的极限也趋近于0；
②定义二：在某一点有定义，在该点极限存在且等于该点的函数值；
③定义三：左极限（右极限）存在且等于该点的函数值，则在该点处左连续（右连续）；
④定义四：在开区间（a，b）内连续，且在a处右连续，b处左连续，则在闭区间【a，b】上连续。

①利用函数连续的定义1、2证明函数在某一点上连续；

②利用函数在某一点连续的充要条件证明分段函数在分界点的连续性、函数在闭区间上的连续性；

初等函数的连续性

连续函数的运算

四则运算

复合函数的连续性
①复合函数的连续性需要两个函数在对应点上都连续；
②复合函数连续时，函数符号与极限号可以变换次序。

反函数的连续性：
若函数在某区间上连续，且是单调递增（递减）；那么对应的反函数在对应区间上连续，且单调性不变。

初等函数的连续性：
①基本初等函数在其定义域内都是连续的；
②初等函数在其定义区间内都是连续的。
（分段函数多数不是初等函数，在其定义域内不一定全是连续的）

函数间断点的类型

①间断点是指在某一点的去心领域内有定义，但在该点不连续；
②在某一点有定义、该点的极限存在（左右极限有一个不存在、左右极限存在但不相等）、该点的极限等于该点的函数值其中至少有一个不成立。

分类

第一类间断点
【左、右极限都存在】