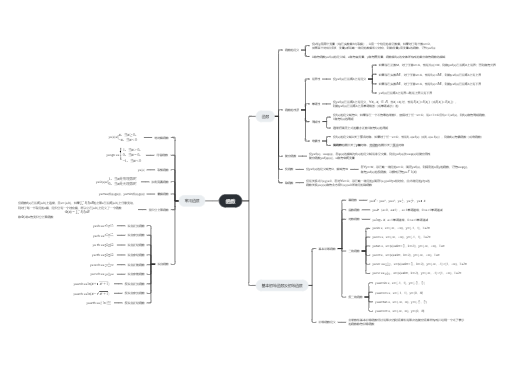
定义域和对应原则是基本要素,两个函数两者相同为同一函数
复合函数(里值域与外定义域交集非空)
同一直角坐标系,y=f(x)与反函数x=f-1(y)重合,y=f(x)与y=f-1(x)关于y=x对称
幂函数 y=x^a,a为实数
指数函数 y=a^x,a>0,a≠1
对角函数 y=logaX,a>0,a≠1
三角函数 y=sinx,y=cosx,y=tanx,y=cotx,y=secx,y=cscx
反三角函数 y=arcsinx,y=arccosx,y=arctanx
基本初等函数经过有限次四则运算和函数复合步骤构成的,可用一个式子表现出
-1,x<0
符号函数sgnX=0, x=0
1, x>0
|x|=x·sgnx
1,x∈Q
狄利克雷函数 D(x)=
0,x∉Q
[x]≤x
[x+m]=[x]+m,m为整数
单调增(严格单调增)x1<x2→f(x1)<f(x2)
单调不减(单调增) x1<x2→f(x1)≤f(x2)
判定:1)定义
2)导数 f(x)在区间I可导,导数>0→单调增
导数≥0 ⇋单调不减
应用:1)根的个数
2)不等式:f(a)=0,单调增→f(x)>0,x∈(a,b]
单调不减→f(x)≥0,x∈(a,b]
奇函数:sinx,tanx,arcsinx,arctanx,ln(1-x/1+x),
ln(x+√1+x²),e^x-1/e^x+1,f(x)-(f-x)
偶函数:x^2,|x|,cosx,f(x)+(f-x)
判定:1)定义
2)f(x)奇函数→导数偶函数
f(x)偶函数⇋导数奇函数
3)连续奇的原函数都是偶,连续偶原函数只有一个奇
f(x)奇,0-X的积分为偶;f(x)偶,0-X的积分为奇
f(x)奇,a-X的积分为偶。
f(x)周期为T,f(ax+b)周期为T/|a|
判定:1)定义
2)可导周期函数的导也是周期
3)周期原函数不一定是周期
f(x)连续,周期T,0-X上积分原函数为周期函数⇋0-T积分为0
即周期函数原函数是周期充要条件是其在一个周期上的积分为0
|arccosx≤π|
判定:1)利用定义
2) f(x)在[a,b]上连续→f(x)在[a,b]上有界;
3) f(x)在(a,b)上连续,且 f(a+)和f(b-)存在→ f (x)在(a,b上有界;
4) f'(x)在区间I(有限)上有界→ f(x)在I上有界
3)中的区间(a,b)改为无穷区间(-∞,b),( a,+∞),(-∞ ,+∞)结论仍成立
1)只有有限个X(最多N个)落在极限a的(a-ε,a+ε)之外
2)极限是否存在以及极限值与数列前有限项无关
3)n→∞=n→+∞
1)x→∞=|x|→∞
2)极限是否存在及极限值仅仅与fx在去心邻域内的函数值有关3)极限=A⇋左右极限均=A
需要区分左右极限:分段函数分界点处;e的∞次;arctan∞;有绝对值的
fx在x0处极限存在→在x0局部有界(反推不成立)
A>0→去心邻域fx>0
去心邻域fx≥0→A≥0
fx>0→A≥0
保序性:A>B→去心邻域fx>gx
去心邻域fx≥gx→A≥B
极限保函数值,函数值保极限
limfx=A⇋f(x)=A+α(x),limα(x)=0
夹逼准则
单调有界准则
概念
高阶
同阶
等价
k阶
概念
常用无穷大比较
无穷大量与无界变量
概念
第一类间断点
第二类间断点
有界性
最值性
介值性
零点定理
复合函数
注意:导数定义与保号性的结合使用P8
奇·奇=偶,奇·偶=奇,偶·偶=偶
概念、性质、存在准则
利用有理运算法则
利用基本极限
利用等价无穷小代换
利用洛必达
泰勒公式
夹逼准则
定积分定义
单调有界准则
中值定理
0/0
∞/∞
∞-∞
0·∞
1^∞
∞^0,0^∞
不定式
n项和的数列极限
n项连乘的数列极限
递推关系
确定极限式中的参数
无穷小量阶的比较
讨论连续性及间断点类型
介值定理、最值定理及零点定理的证明题
关联