=n(n−1)(n−2)⋯(n−m+1)=,n,m∈,并且m≤n。
举例:=654=120。(从下标开始乘,依次递减,乘上标那么多数。)
与顺序有关。
举例:===20。
与顺序无关。
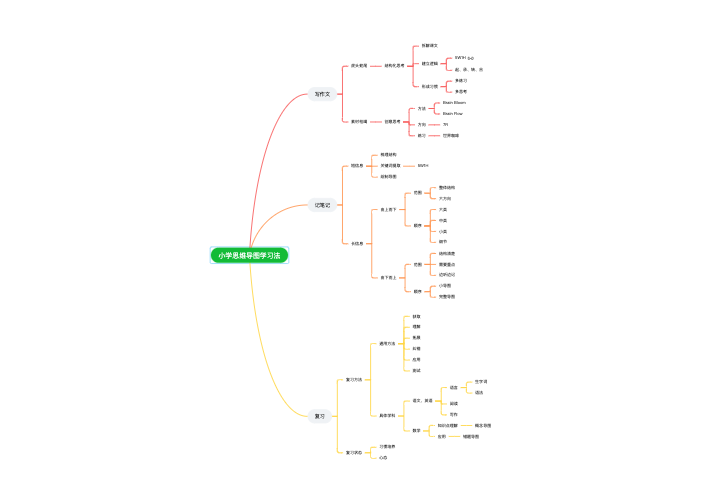
当题目出现“相邻”“在一起”“连续”等要求时,考虑捆绑法。
把相邻的元素捆绑起来,注意内部有无顺序。
将捆绑后的元素看成一个元素,与其他元素进行后序排列。
当题目中出现“间隔”“不相邻”“不连续”等要求时,考虑插空法。
将可以相邻的元素进行排列,排列后形成若干空位。
将不相邻的元素插入形成的空位中。
题目形式为把n个相同的物品分给m个主体,要求每个主体至少分1个时,用插排法。
公式:
若要求每个主体至少分a个,可以先给每个主体分(a-1)个,剩余物品分配时,转化为每个主体至少分1个,再应用插板法解决。
当题目要求不能一一对应时,比如:n把钥匙对应n个锁,要求每个锁和一把不能打卡它的钥匙放进一个信封,这就是全错位排列。
错位排列用表示,表示n个数字的全错位排列。
记住:=0,=1,=2,=9,=44,尤其是最后两个数考频很高。
给出情况求概率。
给出概率求概率。
概率=
概率=各步概率的乘积
概率=各类概率的和
概率=1-不满足条件的概率