高等数学思维导图（含数一内容）_思维导图模板

高等数学

第一章：极限与连续

极限

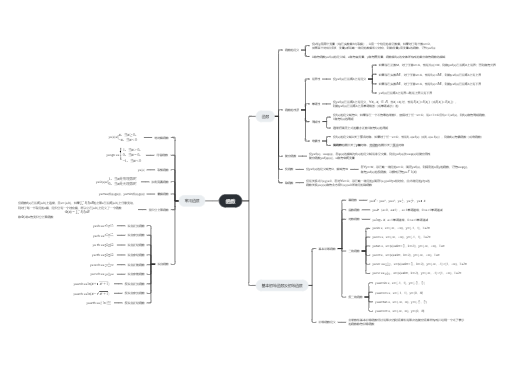
定义：if ∃A，对 ∀ɛ>0，∃0<∣x-a∣<δ，使得 ∣f(x)-A∣<ɛ 成立，则称A为函数
f(x)在 x=a 处的极限，记作 lim₍x→a₎ f(x) = A。

函数在x=a处，极限存在的充要条件是：左右极限存在且相等，
即 f(a-0)=f(a+0)。

性质

唯一性

保号性：若函数f(x)在 x=a 处的极限存在，当0<∣x-a∣<δ，函数在该去心邻域内的正负与极限的正负保持一致。

有界性：if lim₍x→∞₎ an = A，则∃M>0，使得∣an∣≤M，M称之为数列{an}的界。（在级数部分会用到）

极限的存在性质

准则1——迫敛定理

解题思路：找到两个极限相等的数列或函数将所要求的对象夹住。

准则2——单调有界的数列必有极限

解题思路：先证明单调性，再找上界或下界。

无穷小

无穷小量的比较

考点：计算极限时带入常见的等价无穷小简化计算。

连续

定义

函数在闭区间（【a，b】）上连续

f(x)在 (a，b) 上处处连续；

f(a+0)=f(a)，f(b-0)=f(a)；

函数在一点（x=a）上连续

lim₍x→a₎ f(x) = f(a) 或 f(a-0)=f(a+0)=f(a)；

函数f(x)∈ c【a，b】的性质（函数在区间内恒连续）

性质1：∃最大值 M 和最小值 m （最值）；

性质2：∃M₀>0，使得∣f(x)∣≤M₀（有界）；

性质3： ∀η ∈【m，M】，∃ξ∈【a，b】，使得f(ξ)=η（介值定理）；

性质4：若 f(a)*f(b)<0，则∃c∈(a，b)，使得f(c)=0（零点定理）。

连续函数的运算

四则运算：两连续函数进行四则运算后的函数仍然连续

复合函数：设y=f(μ)，μ=φ(x)，且φ(x)≠a

若lim₍μ→a₎ f(μ)=A，lim₍x→x₀₎ φ(x)=a；则 lim₍x→x₀₎ f[φ(x)]=A。

若im₍μ→a₎ f(μ)=f(a)，lim₍x→x₀₎ φ(x)=a；则 lim₍x→x₀₎ f[φ(x)]=f(a)。

间断

定义：若lim₍x→a₎ f(x) ≠ f(a)，则称 x=a 为f(x)的间断点

间断点的分类

第一类间断点：左右极限均存在，且不等于f(a)

可去间断点：f(a+0)=f(a-0)≠f(a)

跳跃间断点:：f(a+0)≠f(a-0）

第二类间断点：左右极限至少有一个不存在

第二章：导数与微分

导数

定义：函数y=f(x)在点x₀处的某领域内有定义，若①lim₍x→x₀₎ [f(x)-f(x₀)/x-x₀]∃，则称函数f(x)在 x=x₀ 处可导，记为f'(x)。(②f'(x)=lim₍∆x→0₎) ∆y/∆x=lim₍∆x→0₎) ∆y/∆x=lim₍∆x→0₎) [f(x₀+∆x)-f(x₀)/∆x]。

函数在f(x)在x=a处可导的充要条件是左右导数存在且相等

性质

可导一定连续，连续不一定可导

求导后会改变函数的奇偶性

求导四大工具

基本公式

四则运算法则

复合函数链式求导法则

反函数求导法则

求导类型（考察题型）

利用定义研究导数

显函数求导

隐函数求导

参数方程确定的函数求导

分段函数求导

先讨论关键点是否连续，确定连续后再判断函数各个部分是否可导。

求函数高阶导

一般使用数学归纳法解决。

微分

可微

定义：设y=f(x) (x∈D)，x₀∈D。若∆y=A∆x+৹(∆x)，则称f(x)在x=x₀处可微。

性质

可微一定可导，可导一定可微（充要条件）

若∆y=A∆x+৹(∆x)，则A=f'(x₀)，即dy∣₍x=x₀₎=f'(x₀)dx

dy=df(x)=f'(x)dx

第三章：微分中值定理与导数的应用

微分中值定理

罗尔中值定理（Rolle）

拉格朗日中值定理（Lagrange）

柯西中值定理（Cauchy）

泰勒中值定理（Talor）

记住常规的x=0处时的麦克劳林公式

洛必达法则

函数的单调性与曲线的凹凸性

函数单调性

判定定理：设函数f(x)∈c【a，b】，且在(a，b)上可导

若f'(x)<0，则递减。

若f'(x)>0，则递增。

驻点：函数一阶导数为0的点（单调性可能发生改变）

曲线凹凸性

定义：设x1,x2∈D，且x1≠x2

凹函数：f(x1+x2/2)<[f(x1)+f(x2)]/2

凸函数：f(x1+x2/2)>[f(x1)+f(x2)]/2

判定定理：设函数f(x)∈c【a，b】，且在(a，b)上二阶可导

若f''(x)<0，x∈(a，b)，则f(x)在【a，b】上是凸函数。

若f''(x)>0，x∈(a，b)，则f(x)在【a，b】上是凹函数。

拐点：函数二阶导数为0的点或二阶导数不存在的点（凹凸性一定发生改变）

考点：求极限

导数的应用

极值点

性质

若f(x)在x=a处取极值，则f'(a)=0或f'(a)不存在。

若f(x)在x=a处取极值，且在x=a处可导，则f'(a)=0。

极小值：∃δ>0，当0<∣x-a∣<δ，若f(x)>f(a)，则称x=a为极小点，f(a)为极小值

极大值：∃δ>0，当0<∣x-a∣<δ，若 f(x)

判别法

①判断点（f'(x₀)=0，此处默认f'(x₀)是存在的）左右的单调性（单调性质）

②设f'(x₀)=0，利用凹凸性确定该点的二阶导数的正负，通过极限保号性得出一阶导数的正负，从而转为①中的情况（凹凸性质）

最值

渐近线

水平渐近线：设曲线L：y=f(x)，若lim₍x→∞₎ f(x) = A，则称此 y=A 为曲线L的水平渐近线。

铅直渐近线：设曲线L：y=f(x)，若lim₍x→a₎ f(x) = ∞，则称此 x=a 为曲线L的铅直渐近线。

斜渐近线：设曲线L：y=f(x)，若lim₍x→∞₎ f(x)/x = a，lim₍x→∞₎ [f(x)-ax] = b，则称此 y=ax+b 为曲线L的斜渐近线。

第四章：不定积分

定义：设F(x)为f(x)的一个原函数，易知 F(x)+C（C为常数）为f(x)所有的原函数。称F(x)+C为函数f(x)的不定积分，记作∫ f(x) dx，即∫ f(x) dx = F(x)+C。

求不定积分的工具

不定积分基本公式

熟记公式

积分法

换元积分法

第一类换元积分法

第二类换元积分法

Case 1：无理数有理化

Case2：平法和差

分部积分法：∫ μ dν = μν - ∫ ν dμ

Case1：被积函数为幂函数与指数函数（后）之积

Case2：被积函数为幂函数与三角函数（后）之积

Case3：被积函数为幂函数（后）与对数函数之积

Case4：被积函数为幂函数（后）与反三角函数之积

Case5：被积函数为指数函数与 sin bx（或 cos bx）之积（都可以去后面，令原式为I，做分部积分直到等式右边出现I，再移项即可）

Case6：被积函数为 sec x（或 csc x）的奇次方（都可以去后面，令原式为I，作分部积分直到等式右边出现I，再移项即可）

第五章：定积分

定义（含推导背景——求曲边梯形的面积）：
1、分割区域；
2、表示单个微元的面积 ∆Si = f(ξi)∆xi，进而表示整个区域的面积S（此处为≈）；
3、取 λ = max{∆x1，∆x2，∆x3，...，∆xn}，则 S = lim₍λ→0₎ ∑ f(ξi)∆xi。

①L：y=f(x)≥0，x∈【a，b】，则面积 A = ∫₍a，b₎ f(x) dx；

②lim₍λ→0₎ ∑ f(ξi)∆xi 与【a，b】的分法以及ξi的取法无关；

③f(x)在【a，b】上有界（必要条件）不一定可积；

④若f(x)∈c【a，b】，则可积；

⑤若f(x)在【a，b】上只有有限个第一类间断点，则可积。

一般性质

①加减性质

②公共常数可提取

③∫₍a，b₎ 1 dx = b-a

④若f(x)、∣f(x)∣在【a，b】上可积，则∣∫₍a，b₎ f(x) dx∣ = ∫₍a，b₎ ∣f(x)∣ dx

⑤积分的介值定理：m(b-a)≤∫₍a，b₎ f(x) dx≤M(b-a)

⑥积分中值定理

积分基本定理

①d/dx ∫₍a，x₎ f(x) dx= Φ'(x) = f(x)（Φ(x)为积分上限函数）

②牛顿——莱布尼兹公式（∫₍a，b₎ f(x) dx = F(b)-F(a)）

③积分中值定理的推广

定积分的换元积分法和分部积分法

特殊性质

奇偶性质

平移性质

关于sin x（或cos x）的函数性质

点火公式（区间范围为0到π/2）

反常积分

积分区间无限型反常积分（区间有问题）

Case1：[a，+∞）

Case2：(-∞，a]

Case3：(-∞，+∞)

判别方法

定义法（即用上三种情况计算）

判别法

处理无穷处反常积分的方法：先取无穷内的正常点，在对此正常求得的积分值求极限（反常化正常），此极限值即为此反常积分的收敛对象（若极限趋于无穷，则该反常积分发散）

无界函数的反常积分（瑕积分，含间断点，该间断点称为瑕点）（函数有问题）

Case1：(a，b]（左边界为瑕点）

Case2：[a，b)（右边界为瑕点）

Case3：[a，c)∪(c，b]（区间内的点为瑕点）
（其收敛的充要条件为两部分积分均收敛）

判别方法

定义法（算）

判别法

对瑕点进行正常化处理，也是用极限逼近

补充

Γ函数：形如

特性

柯西积分不等式

定积分的应用

几何应用

面积

体积

元素法

第六章：微分方程

定义：含有导数或微分的方程，称为微分方程。

一阶微分方程

可分离变量的微分方程

解法

齐次微分方程

解法

一阶齐次线性微分方程

形如

通解公式

一阶非齐次线性微分方程

形如

通解公式

可降阶的高阶微分方程

y⁽n⁾ = f(x)型

解法：直接对高阶导数逐步还原即可

缺y型

解法

缺x型

解法

高阶线性微分方程（以二阶为主）

基本概念

二阶齐次线性微分方程

形如：*

二阶非齐次线性微分方程

形如：**

线性相关与线性无关：设φ1(x)，φ2(x)为两个函数

若两者不成比例，则称为两者线性无关

若两者成比例，则称两者线性相关

二阶线性微分方程解的结构

齐 + 齐 = 齐

齐 + 非齐 = 非齐

非齐 + 非齐 = 齐

（拆解性质）对于方程**，若f(x)=f1(x)+f2(x)（即可拆成两部分），则分别构造两个二阶非齐次线性微分方程，且φ1(x)，φ2(x)分别为它们的特解，则有原方程特解为：
y=φ1(x)+φ2(x)

（系数和的特点）设φ1(x)，φ2(x)，...，φn(x)，为方程**的解，则通解的组合形式为y=k1φ1(x)+k2φ2(x)+...+knφn(x)

若y为方程*的通解，则k1+k2+...+kn=0（系数和为0）

若y为方程**的通解，则k1+k2+...+kn=1（系数和为1）

（二阶常系数线性微分方程通解形式推导定理）
①若φ1(x)，φ2(x)为方程*的两个线性无关的解，则方程*的通解为：
y=C1φ1(x)+C2φ2(x)（C1，C2为任意常数）；
②若φ1(x)，φ2(x)为方程*的两个线性无关的解，φ0(x)为方程**的特解。
则方程**的特解为：
y=C1φ1(x)+C2φ2(x)+φ0(x)（C1，C2为任意常数）;

二阶常系数线性微分方程的解

二阶常系数齐次线性微分方程

形如

补充：λ² + pλ + q =0，为它的特征方程，根据其Δ的情况通解分为三种情况

通解

Δ>0，通解形式

Δ=0，通解形式

Δ<0，通解形式

二阶常系数非齐次线性微分方程

形如

补充：非齐次的通解为齐次部分的通解与非齐次部分特解的组合

类型一：

特解：k ≠ λ1 ，k ≠ λ2；→ 不添 x

特解；k = λ1 ，k ≠ λ2；→ 添 x

特解：k = λ2 = λ1；→ 添 x²

类型二：

特解：α+iβ ≠ λ1 ，α+iβ≠ λ2；→ 不添 x

特解：α+iβ = λ1 ，α+iβ≠ λ2；→ 添 x

全微分方程

形式

判定条件

通解形式

补充解法

欧拉方程

形如

解法

引入微分算子简化计算

伯努利方程

形如

解法

第七章：多元函数微分学

基本概念

邻域与去心邻域

二元函数的极限

二元函数的连续性

偏导数

偏增量与全增量

偏导数

高阶偏导数

二元函数连续、可偏导、可微之间的关系

一节偏导连续>可微>可偏导、连续（含证明）

可微 → 连续（易）

可微 → 可偏导（易）

一阶偏导连续 → 可微（难）

多元函数求导法则

复合函数求导法则

定理一：设z=f(μ)连续可导，μ=φ(x，y)对x，y可偏导，则复合函数z=f[φ(x，y)]对x，y可偏导；

定理二：设z=f(μ，ν)连续可偏导，μ=φ(t)，ν=ψ(t)对t可导，则复合函数z=f[φ(t)，ψ(t)]对t可导；

定理三：设z=f(μ，ν)连续可偏导，μ=φ(x，y)，ν=ψ(x，y)对x，y可偏导，则z=f[μ=φ(x，y)，ν=ψ(x，y)]对x，y可偏导；

隐函数（组）确定的函数求导法则

补充：隐函数存在定理

求导法则

定理一：

定理二：

定理三：

补充：克莱姆法则（线代）

多元函数的极值

无条件极值

定义：给定二元函数z=f(x，y)，其中定义域D为开区间，求z=f(x，y)在D上的极值，即无条件极值。

判定定理

定理一（必要条件）：设z=f(x，y)在定义域D内连续可偏导，若(x₀，y₀)为函数极值点，则 fx(x₀，y₀) = 0，fy(x₀，y₀) = 0；

定理二（充分条件）：设z=f(x，y)在定义域D内二阶连续可偏导，且(x₀，y₀)为函数驻点；

条件极值（二元函数）

定义：函数z=f(x，y)在等式条件 φ(x，y) = 0 下的极值，即条件极值

求解方法

拉格朗日乘数法

参数方程法

多元微分学反问题

多元函数微分学的几何应用

方向导数

二元：z=f(x，y)

三元：μ=f(x，y，z)

梯度

第八章：二重积分（含三重积分）

概念

性质

加减拆分

常数提取

面积 A = ∫∫ 1 dxdy

对称性

关于x轴

关于y轴

关于 y=x

二重积分的中值定理：设二元函数f(x，y)在平面有界区间闭区域D上连续，且D的面积为 A，则∃(ξ，η)，使得：
∫∫(D) f(x，y) dxdy = f(ξ，η)*A

计算方法

直角坐标法

X型区域

Y型区域

极坐标法

三重积分

定义

性质：与二重积分相同，但要升高一个维度，即面积变体积

计算方法

铅直投影法：先一后二

切片法：先二后一

球面坐标法

第九章：空间解析几何

向量及运算

定义

向量的坐标

方向角、方向余弦

运算

几何刻画

加减

k倍

数量积（点乘）

符合交换律

两不为零的向量点乘为0，则两向量垂直

向量积（叉乘）

符合交换律

所得的积向量与叉乘的两向量均垂直

若两非零向量叉乘为0向量，则两向量平行

向量a X 向量b 的模等由它们围成的三角形面积的两倍

代数刻画

加减

k倍

数量积：对应项相乘再累加

向量积：做行列式运算（对三阶有简便方法）

向量的应用

空间曲面

一般形式：
Σ：F(x，y，z) = 0

特殊曲面

柱面：
Σ：F(x，y) = 0

旋转曲面的变换

二维

三维

退化——平面

点法式

截距式

一般式

空间曲面问题

在某点的切平面

在某点的法向量

空间曲线

形式

一般式

参数式

退化——直线

点向式

参数式

一般式

空间曲线问题

求某点的切线

求某点的法平面

距离问题

点点之距

点线之距

点面之距

线面之距（同点面距离）

平行平面之距

异面直线之距

判断是否异面

方法

第十章：曲线与曲面积分

曲线积分

第一类曲线积分

定义背景：求密度不均匀的曲线质量∫L ρ(x，y) ds，称为函数f(x，y)在L上对弧长的曲线积分；

两种形式的弧微分推导

性质

加减

常数可提取

区域可分

∫L 1 ds = l（曲线L的长度）

对称性

关于x轴

关于y轴

关于y=x

计算方法

定积分法

一般型

参数型

第二类曲线积分

定义背景：做功

Case1：二维空间路径与作用力均理想

Case2：二维空间路径与作用力均不理想

Case3：三维空间路径与作用力均不理想

性质

加减

常数可提取

线段区域可分

∫L- = -∫L；

对称性

关于x轴

关于y轴

关于y=x

计算方法

定积分法

一般式

参数式

二重积分法（格林公式）

单连通区域

多连通区域

定理：
若①D为xOy面内的连通区域，L为边界；
②P(x，y)，Q(x，y)在区域内连续可偏导；
则有：

解题思路：若为连通区域则直接使用公式即可；若非连通区域则需要补为连通区域（注意补上线的方向正负问题）。另外在所给的区域D内可能会存在某个点不能使P，Q连续可偏导（或在该点无定义），此时可在D内再取一个区域D1，将该点包住，此时区域D被分为两部分（D1与D2），再进行相应的转化即可。

子主题4

曲线积分与路径无关问题

四个等价条件

∫L P dx + Q dy 与路径无关

任取闭曲线C⊂D，有∫C P dx + Q dy = 0

柯西黎曼条件成立

∃μ(x，y)，使 P dx + Q dy= dμ（即存在一个全微分方程）

曲面积分

第一类曲面积分

定义

性质

加减

常数可提取

区域可分

∫∫∑ 1ds = A（面积）

对称性

关于x轴

关于y轴

关于y=x

计算方法

二重积分法

第二类曲面积分

定义

性质

加减

常数可提取

区间可分

∫∫∑- = -∫∫∑

对称性

关于x轴

关于y轴

关于y=x

计算方法

二重积分法

高斯公式

两类曲面积分的转化

积分中域与界的关系

高斯公式

定理（含证明）：设空间区域Ω由分片光滑的双侧封闭曲面S围成，取S外表面。若函数P，Q，R在Ω上连续，具有一阶连续偏导数，则有：

斯托克斯公式

定理：设光滑曲面S的边界L是一段光滑的连续曲线。若函数P，Q，R在S上连续，且具有一阶连续偏导数，则有：

右手法则：定方向

场论初步：设向量A={P(x，y，z)，Q(x，y，z)，R(x，y，z)}

散度

旋度

流量

环流量

第十一章：无穷级数

常数项级数

定义

性质

两收敛的级数（设分别收敛于A，B）加减后的结果收敛性不变，且收敛于A(+-)B

常数可提取

级数增加、减少有限项不改变其收敛性，但所收敛的值可能会改变

（加括号提升收敛性）若一个级数收敛，则任意添加括号后的级数也收敛；反之，若一个级数添加括号后收敛，不一定原级收敛

（级数收敛的必要条件）若级数收敛，则其一般项在n趋于无穷时的极限为零

两个重要对象

P级数

几何级数：即无限等比数列之和

正项级数

定义

可联想到数列极限的有界性

敛散性判别法

比较审敛法

基本形式

极限形式

比值法

根值法

交错级数

定义

判别法——莱布尼兹判别法

绝对收敛与条件收敛

绝对收敛→收敛

幂级数

定义

幂级数的收敛区间

阿贝尔定理

收敛半径的计算

性质

和函数概念

和函数（若和函数在开区间连续）在开区间端点的连续性

和函数的逐项可导性

和函数的逐项可积性

将函数展成幂级数

直接法

记忆：麦克劳林级数（7个）

特别地，有

间接法

思路：依照题目要求的形式，向公式形式靠

求和函数（难）

型一：∑P(n)x^n

求法：往两种分数型公式靠

型二：∑x^n/P(n)

求法：往两种ln型公式靠

傅里叶级数

形式：f(x)以2π为周期

狄利克莱充分条件：
f(x)连续或存在有限个间断点；
f(x)存在有限个极值点；
则：
f(x)可以进行傅里叶展开（即式*）；
当x为第一类间断点时，式* = 1/2[f(x-0)+f(x+0)]。

计算公式

将定义于 [-π，π] 非周期函数展开成傅里叶级数

思路：进行周期延拓（将非周期函数转为周期函数），再计算

将定义于[0，π]的函数展开成傅里叶级数

思路：进行区间延拓(将区间变为[-π，π])，再进行周期延拓

周期为2l的函数展成傅里叶级数

计算公式

也有以上两种类型，计算思路相同

考点：间断点的分类

考点：求极限

考点：结合增减性、凹凸性，求函数在某一区间内的极值

考点：判断反常积分敛散性、求收敛于某个值

考点：判断函数在区间内的连续性

考点：利用导数定义求解相关问题、求导

考点：证明题

考点：求极值、最值

考点：找函数的渐近线

考点：求积分

考点：证明题

高等数学思维导图（含数一内容）

模板简介

猜你喜欢

相关文章