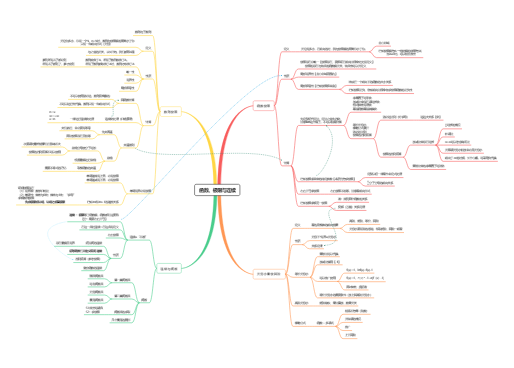
三阶行列式的对角线法
行列式是一个数,他是不同行不同列元素乘积的代数和。
n阶行列式的完全展开式
①逆序:一个排列中,如果一个大的数排在小的数之前(列数);
②逆序数:一个排列的逆序总数;
③偶(奇)排列:一个排列的逆序数是偶数(奇数);
④当列数是偶(奇)排列时,该项前面带正(负)号;
⑤行列式计算:同一列不能取2个,同一行不能取2个。
①经过转置行列式的值不变;
②两行(或两列)互换位置,行列式的值变号;
③某行(列)如有公因子k,则可把k提出行列式记号外;
④把某行(或列)的k倍加到另一行(列),行列式的值不变;
⑤两行(或两列)相同,行列式的值为 0 ;
⑥若某行(或列)的元素全为 0,行列式的值为 0;
⑦若两行(或两列)的元素对应成比例(提取比例系数,得两行相同行列式),行列式的值为 0;
⑧若行列式某行(列)是两个元素之和,则可把行列式拆成两个行列式之和。
①n阶行列式=任何一行(列)元素与其对应的代数余子式乘积之和;
②行列式的任一行(列)元素与另一行(列)元素的代数余子式乘积之和为 0 ;
①主对角线和副对角线方向相反;
②上(下)三角形行列式的值=主对角线元素的乘积;
③拉普拉斯展开式:主对角线=,副对角线=;
④范德蒙行列式:各项差的乘积;
案例
①非齐次线性方程组:系数行列式≠0,则方程组有唯一解;
②是中第 列元素(即的系数)替换成方程组右端的常数项;
③非齐次方程组的解:=()
④齐次线性方程组的系数行列式≠0的充要条件:方程组有唯一零解;
转化为上(下)三角行列式
降阶(行列式按行或列展开)
转化为上(下)三角行列式