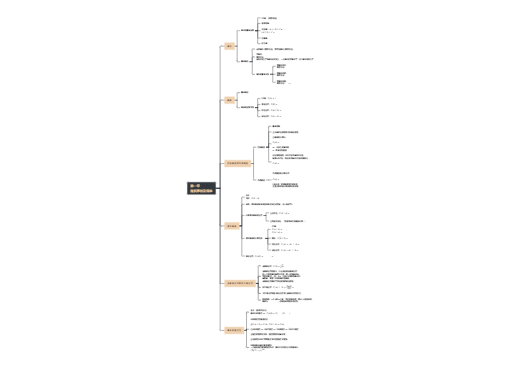
对随机现象进行观察称为随机试验,简称试验,记作 E
(1)可以在相同条件下重复进行;
(2)所有可能结果事前可知;
(3)试验之前不能确定哪个结果会发生.
随机试验的结果称为随机事件,简称事件,记作 A , B , C .每次试验必然发生的事件称为必然事件,亦称样本空间,记作 Ω .样本空间中的元素称为样本点,亦称基本事件,记作ω . 每次试验不可能发生的事件称为不可能事件,记作 Φ .
(1)包含:若事件 A 发生,事件 B 一定发生,则称 B 包含 A 或 A 包含于 B ,记作 A ⊂ B .
特别地,若 A ⊂ B 且 B ⊂ A ,则称 A 与 B 相等,记作 A = B ;
(2)和:事件 A 与 B 至少有一个发生,称为 A 与 B 的和,记作 A U B ;
(3)积:事件 A 与 B 同时发生,称为 A 与 B 的积,记作 AB ;
(4)互不相容(互斥):若事件 A 与 B 不能同时发生,即 AB = Φ ,则称 A 与 B 互不相容;
(5)对立(互逆):若事件 A 与 B 不能同时发生,但必有一个发生,即 A U B = Ω 且 AB = Φ ,则称A 与 B 对立,
(6)差:事件 A 发生但事件 B 不发生,称为 A 与 B 的差,记作 A − B ,
(1)交换律 A U B = B U A, AB = BA;
(2)结合律 AU(B U C) = (A U B) U C , A(BC) = (AB)C ;
(3)分配律 A U (BC) = (A U B)(A U C) , A(B UC) = (AB) U (AC) ;
(4)摩根律
(5)吸收律 AU(AB) = A , A(A U B) = A .
设试验的样本空间为 Ω ,称满足下列条件的事件集上的函数 P(⋅) 为概率:
(1)(非负性)对任意事件 A ,有 P(A) ≥ 0 ;
(2)(规范性) P(Ω) = 1;
(3)(可列可加性)
【评注】上述为概率的公理化定义,实际上我们可以简单地把概率看作试验中事件发生的可能性大小.
若 A ⊂ B ,则 P(A) ≤ P(B) ;
P(A U B) = P(A) + P(B) − P(AB) ;
P(A U B U C) = P(A) + P(B) + P(C) − P(AB) − P(BC) − P(AC) + P(ABC)
P(A − B) = P(A) − P(AB) ;
(1)加法原理
(2)乘法原理
【评注】加法原理与乘法原理得区别在于前者完成任何一类方法即完成一件事,后者须 n 步都完成才算完成一件事,亦可简单地概括为“分类加法,分步乘法”.
(3)排列
(4)组合
设试验只有有限个等可能的样本点,称此试验为古典概型,事件 A 的概率为
设试验的样本空间为某区域,事件发生的可能性与其对应的几何度量成正比,称此试验为几何概型,事件 A 的概率为
一维:长度
二维:面积
三维:体积
【评注】设试验分为两步,第一步有 n 种情况( B1, B2 ,…, Bn 构成完备事件组).若求第二步中事件 A的概率,则用全概率公式;若已知事件 A 发生,求在第一步哪种情况下发生的概率,则用贝叶斯公式.
设随机事件 A , B 满足 P(AB) = P(A)P(B) ,称 A 与 B 相互独立.
(1)0 概率事件或 1 概率事件与任意事件相互独立,从而不可能事件或必然事件与任意事件相互独立;
(2)若事件 A 与 B 既相互独立又互不相容,则 A 与 B 至少有一个为零概率事件.
(1)事件 A1 , A2 ,…, An 相互独立一定两两独立,反之不成立;
(2)设事件 A1 , A2 ,…, An 相互独立,则由部分事件所产生的事件与由其余事件所产生的事件相互独立.