3-稳恒磁场（大学物理）_思维导图模板

稳恒磁场

稳恒电流

电流

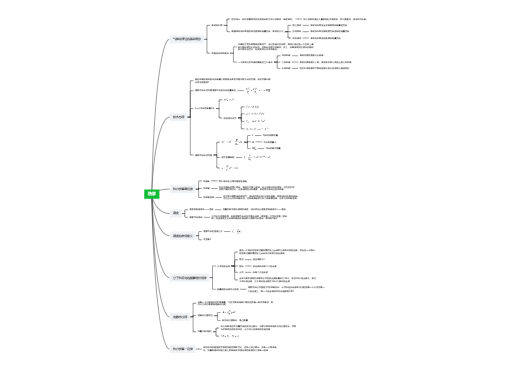
电流：大量带电粒子定向运动形成的

载流子：形成电流的带电粒子。如：自由电子、离子、空穴等

电流强度：单位时间内通过导体某一截面的电量，简称为电流，

SI：安培（安） 1A = 1C/s

方向：正电荷的运动方向

稳恒电流：通过导体任一截面的电流 I 不随时间变化

电流密度

电流密度：单位时间内通过垂直于正载流子运动方向的单位面积的电量，为矢量，，其中 n 是金属单位体积电子数，是金属的特征量

SI：

电流是电流密度的通量

通过封闭曲面的电流

电流的连续性方程

电流的稳恒条件

欧姆定律的微分形式

推导过程

式1，

式2，

式3，，电阻定律，是电阻率

式4，，是电导率

式5，

将式1—4带入式5，得到欧姆定律的微分形式

电源及电源的作用

非静电力：不断把负极板上的正电荷搬运回正极板，并维持两极板上的电荷分布不变，从而在导线中产生一个稳恒电场

电源：任何能够提供非静电力，并能够把其他形式的能量转换成电能的装置。

电源结构示意图

非静电场场强

电动势

电动势：把单位正电荷经电源内部由负极移向正极过程中非静电力所做的功，反应非静电力做功本领

SI：伏特(V)

电动势并不是矢量，但通常规定电源内从负极到正极的方向为电动势的方向。

磁场磁感应强度

磁的基本现象

磁体有两极：北极(N极)和南极(S极)，同极相斥，异极相吸

地球的N极在地理南极附近， S极在地理北极附近，存在磁偏角

安培：“分子电流假说”

磁性物质中的每个分子都可视为环形电流，称为分子电流。当这些分子电流做定排列时，在宏观上就会显示出磁性， N极和S极分布在环形电流的两侧

磁力是运动电荷之间相互作用的表现

磁场与磁感应强度

磁场：运动电荷会产生磁场，磁场又会对其中的运动电荷产生力的作用

磁感应强度

运动电荷在磁场中受力

大小：

方向：右手螺旋定则

磁感应强度的大小

SI：特斯拉(T) 1 T=1N/A•m

磁感线 Magnetic Field Lines

磁感线

磁感线上每一点的切线方向表示该点的方向

磁场中某点通过垂直于的单位面积的磁感线条数等于该点处磁感应强度的大小

磁感线的特点

无头无尾的闭合曲线

与电流套连

与电流成右手螺旋关系

直导线，则拇指方向是电流方向，四指方向是磁感线方向

螺线管，则拇指方向是磁感线方向，四指方向是电流方向

毕奥—萨伐尔定律

毕奥—萨伐尔定律：真空中电流元在场点 P 产生的磁感应强度为，其中是真空磁导率，且

大小：

方向：垂直于由和决定的平面，四指从绕过小于 180 度角转向，拇指方向就是磁场方向（右手螺旋定则）

讨论

对一段闭合载流导线，有

毕奥—萨伐尔定律中的电流元是指闭合稳恒电流中某一电流元，它是不能单独存在的

毕奥—萨伐尔定律在稳恒磁场中的地位和作用，有如库仑定律在静电场中的地位和作用。利用毕奥—萨伐尔定律和叠加原理，可以导出稳恒磁场的高斯定理和安培环路定理。这是稳恒磁场所遵从的两条基本规律。

毕奥—萨伐尔定律的应用

应用一：直电流的磁场

已知：场点 P 到载流直导线的距离为 r

方向：右手定则

讨论

无限长载流直导线，

半无限长载流直导线，场点 P 在端点的垂直线上，

场点 P 在直电流的延长线上，此时

应用二：平板的磁场

已知：金属薄板宽为 b，无限长，电流为 I 且均匀分布。点 P 在过金属板中分线的垂线上，到金属板的距离为 d，点 P' 与金属板共面，到金属板中分线的距离为 a

平板外场点 P：

方向

磁场方向沿 x 轴方向

金属平板两侧等距处，磁感应强度大小相同，方向相异

讨论

场点 P 距平板无限远，即 d>>b，此时

此时，金属板可以等效看作无限长载流直导线

金属平板无限大，即 d<

，表示面电流密度，因为关于电流方向作金属板的截面，则每一个截面电流强度都是 I，因此单位面积的电流强度就是 I/b

平板平面场点 P'：

应用三：圆形载流线圈轴线的磁场

已知：载流线圈电流为 I，半径为 R，求解其轴线上的磁场分布

方向：磁感线方向沿着 x 轴正方向，可以使用右手定则进行判断

讨论

场点在环心处，x=0

半圆弧电流圆心处

弧度为的任意圆弧圆心处

圆形载流导线为 N 匝时

应用四：螺线管轴线的磁场

已知：均匀密绕螺线管，长度为 L，半径为 R，单位长度上绕有 n 匝线圈，且通有电流 I，求其轴线上的磁场分布

方向：磁场方向和电流的绕向呈右手螺旋关系

讨论

无限长直螺线管，即 L>>R，此时

场点在长直螺线管任一端口的中心处，此时

运动电荷的磁场（对单个电荷而言）

公式推导示意图

运动电荷产生磁场示意图

例题

磁场的高斯定理和安培环路定理

磁通量

磁通量：通过一给定曲面的总磁感线数

微分式

积分式

SI：韦伯（Wb）

磁场的高斯定理

安培环路定理

定理表述：在恒定电流的磁场中，磁感应强度沿任意闭合路径的线积分等于路径所包围的电流强度的代数和的倍

讨论

如果电流的方向与回路的绕行方向(积分方向)成右手螺旋关系，则电流为正，反之为负

被包围的电流指的是与 L 套合的电流

电流与 L 多次套合，则套合一次就被包围一次

是空间中所有稳恒电流共同产生的，只不过没有被套合的电流对环路积分没有影响罢了

安培环路定理中的电流必须是闭合稳恒电流，对于一段稳恒电流的磁场不可以用安培环路定理求解。其中无限长载流直导线可以近似为闭合稳恒电流，一段稳恒电流的磁场可以考虑使用毕萨定律进行求解。

安培环路定理的应用

应用一：电流均匀分布的无限长金属柱面的磁场分布

问题分析

磁场的对称性：取两个对称的电流微元，其产生的对应的磁场微元大小相等、和矢量方向垂直于径矢，因此，所有电流微元在 P 点产生的总磁感应强度垂直于径矢

磁场分布

应用二：电流均匀分布的无限长圆柱体的磁场分布

问题分析

将柱体看作一系列同轴柱面，每个柱面的磁感应强度分布规律如应用一

磁场分布

应用三：无限大平面电流的磁场分布，面电流密度为 j

问题分析

磁场对称性

积分路径选取

应用四：无限长均匀密绕载流直螺线管内的磁场，设螺线管通有电流 I，单位长度上的线圈匝数为 n

问题分析

假设：可以认为每匝线圈均与轴线垂直，并可视为圆形载流导线

磁场对称性分析

通过对称性分析可知，在距轴线等远处磁感应强度的大小应相等，其方向应与轴平行

积分路径的选取

小结

无限长螺线管内部的磁场是均匀磁场

无限长螺线管外部任一点磁场为零

应用五：螺绕环的磁场，设轴线的半径为 R，环上均匀密绕 N 匝线圈

磁场对载流导线的作用

安培力

微分式

积分式

安培力的应用

应用一：计算两根无限长平行载流直导线之间的相互作用力

同向电流相吸引，异向电流相排斥

应用二：计算载流非直导线在均匀磁场中的受力

前提

解题

均匀磁场中的闭合载流回路整体上不受磁力

应用三：计算载流非直导线在非均匀磁场中的受力

前提

解题

应用四：电磁炮原理

载流线圈的磁矩

公式

讨论

S：平面载流线圈的面积

：平面载流线圈的单位法向量，与电流的方向满足右手螺旋关系

线圈 N 匝，则磁矩变为

单位：

载流线圈在均匀磁场中受的力和力矩

前提：设载流线圈半径为 R，电流为 I，置于均匀磁场中

情形一：磁场方向和线圈法线方向同向

合力为零

合力矩为零

情形二：磁场方向和线圈法线方向垂直

合力为零

合力矩，方向沿 z 轴

情形三：磁场方向和线圈法线方向呈角

合力为零

合力矩

载流线圈在均匀磁场中受的合力为零，合力矩，作用效果是使线圈磁矩的方向转向外磁场方向

磁偶极矩 VS 电偶极矩

磁偶极矩的应用：计算圆盘的磁偶极矩和力矩

磁场对运动电荷的作用

洛伦兹力

公式

讨论

大小：

方向：右手螺旋定则

洛伦兹力和安培力的关系：洛伦兹力是单个电荷的受力，是安培力的微观体现

洛伦兹力的特征

，洛伦兹力只改变粒子速度方向，不改变粒子速度大小

洛伦兹力对粒子不做功

带电粒子在磁场中的运动总是匀速率运动

带电粒子在磁场中的运动

均匀磁场

情况一：

粒子作匀速直线运动

情况二：

粒子作匀速圆周运动

规律

回旋半径

回旋周期

回旋频率

回旋半径与粒子速度成正比，回旋周期与粒子速度无关

应用：回旋加速器

情形三：

粒子作螺旋运动

螺旋半径

螺距

非均匀磁场

粒子一般仍作螺旋运动，但半径和螺距都是变化的

霍尔效应

定义：磁场中载流导体上出现横向电势差的现象

霍尔效应的两种情形

载流子为负

载流子为正

3-稳恒磁场（大学物理）

模板简介

猜你喜欢

相关文章