高中数学_思维导图模板

高中数学

代数

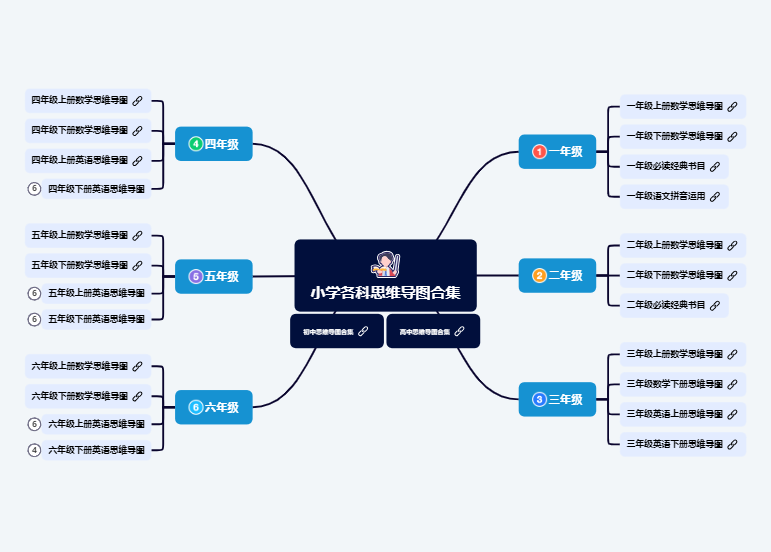
整式

分式

函数

代数方程

不等式

数列

基础概念

数列定义

按一定的次序排列的有规律的一列数

通项

a(n)=f(n)

前n项和

s(n)

a(n)与s(n)的关系

a(n)=

s1 n=1

sn=s(n-1) n>=2

等差等比数列

等差数列

核心元素

a1、d

定义

a(n+1)-an=d

常数列为特殊等差数列

通项

an=a1+(n-1)d

关于n的一次函数

三项

数列a、b、c成等差数列

b=(a+c)/2

角标

如果m+n=s+t

am+an=as+at

求和

sn=(n(a1+an))/2

sn=na1+(n(n-1))/2*d

性质

sn，s(2n)-sn，s(3n)-s(2n),#####仍成等差数列

等比数列

核心元素

a1、q

定义

a(n+1)/an=q

非0常数列为特殊等比数列

通项

an=a1*q^(n-1)

关于n的指数函数

三项

数列a、b、c成等比数列

b^2=ac

角标

如果m+n=s+t

am*an=as*at

求和

(a1(1-q^n))/(1-q) q不为1

na1 q=1

若|q|<1，则该数列的所有项和a1/(1-q)

性质

sn，s(2n)-sn，s(3n)-s(2n),#####仍成等比数列

等差等比数列通项问题

设a1，d或a1，q

等差数列

an=a1+(n-1)d=dn+(a1-d)

an=am+(n-m)d

等比数列

an=a1q^(n-1)

an=amq^(n-m)

等差、等比脚注性质与中项公式

角标性质

角标和相等且对应项数也相等

三项问题

经验

数列a，b，c成等差且等比

a=b=c

注意

等比数列项的正负性

总结

等差数列

已知和

三项

a-d，a，a+d

四项

a-3d，a-d，a+d，a+3d

等比数列

已和积

三项

a/q，a，aq

四项

a/(q^3)，a/q，aq，aq^3

等差数列求和问题

公式1

sn=(n(a1+an))/2

平均数*项数

角标性质*对数

公式2

sn=na1+(n(n-1))/2*d

注意

等差{an}，{bn}的前n项和分别为sn与tn，则ak/bk=s(2k-1)/t(2k-1)

等差数列sn图像、最值、变号问题

图像sn

sn=na1+(n(n-1))/2*d=

d/2*n^2+(a1-d/2)n

关于n的一个二次函数，且常数项为0

d>0

有最小值

d<0

有最大值

sn最值问题

方法1

从通项an角度

a1<0，d>0

sn有最小值

an<=0，a(n+1)>0

求出n

方法2

从sn二次函数角度

sn=na1+(n(n-1))/2*d=d/2*n^2+(a1-d/2)n

对称轴n对=-b/(2a)=-(a1-d/2)/(2*d/2)=1/2-a1/d

特别注意

把sn图形理解成二次函数分析

等差sn变号问题

sn=((a1+an)n)+角标性质分析

等比数列求和

(a1(1-q^n))/(1-q)=（a1-anq）/(1-q) q不为1

na1 q=1

注意

a1/(1-q)-(a1/(1-q))*q^n

=k-kq^n

非等差等比数列

思路

化归到等差等比数列

穷举找规律

总结

转化为等差等比

穷举找规律

数列应用题

经验

区分等差等比数列

区分求an

注意项数

总结

等差等比化归思想

穷举找规律思路

特值法

常数数列

应用题

概述

一般方法

列方程、不等式应用题

应试方法

小学生方法

条件处理

声东击西、多个条件反向验证、条件可以特殊化、比较列表格

应用题中不定方程与不等式

未知量个数大于方程个数

注意

整数解的不定方程，用下列方法可以减少穷举的次数

从系数绝对值大的入手

利用整除性，奇偶性

实际问题表量有范围

价格问题

利润率=利润/进价*100%=（售价-进价）/进价*100%

售价=进价*（1-利润率）

经验

甲、乙以相同的售价卖出，一件赚了P%,一件亏了P%，则最终一定是亏了

平均问题

平均数=总分/总人数

不等式与线性规划应用题

不等式问题

线性规划应用题

实数解线性规划问题

整数解线性规划问题（穷举法）

直线形式

目标函数

约束条件

经验结论

最值一般在边界

斜率的比较

总结

线性规划解题思路

一般方法

由斜率比较大小找最优解

实用技巧

最值一般在约束条件边界点附件找到

集合计数

标数

用公式

两集合

n(A并B)=n(A)+n(B)-n(AB)

三集合

n(A并B并C)=n(A)+n(B)+n(C)-n(AB)-n(AC)-n(BC)+n(ABC)

函数图形应用+分段函数

函数图形截距，距离

分段函数

注意：落入那一段，分段计算

至少至多问题

方法1

>=/<=

不等式/最值

方法2

总量一定

对立面的最值

X Y Z=总量一定

YZ最大，则X求至少=最小

方法3

整数解

平均与极端思想

抽屉原则

至少有一个盒子中不少于2个球

a只球b只盒子，至少有1个盒子不少于a/b的商加1

最不利原理

极端

最值应用题

二次函数

均值不等式

几何

平面几何

三角形面积计算

1/2*底*高

边之比===面积之比

三角函数

利用全等或相似

三角形的四心

内心

角平分线

三角形内切圆的圆心

外心

三边垂直平分线

三角形外接圆的圆心

重心

三边中线

垂心

三边高

特殊三角形

直角三角形、等腰三角形、等腰直角三角形、等边三角形

两个三角形全等或相似

全等

旋转、折叠找全等

相似

平行直接找相似

直角三角形射影定理

CD^2=AD*DB

AC^2=AD*AB

CB^2=BD*AB

四边形

圆

添半径

组合图形

直角三角形的内切圆与外接圆

内切圆

r=(a+b-c)/2

外接圆

R=c/2

圆套圆与方套方

圆套圆

圆方圆

面积之比=2*3.14：4：3.14

方套方

方圆方

面积之比=4：3.14：2

平面几何专题

不规则圆形阴影面积问题

用割补发把不规则图形转化为规则图形

注意

熟悉与圆有关的一些图形

图形的重叠、对称、平移

总结

平面几何应试技巧

量，有图有真相

量答案

加条件

添

三角形加高

四边形加高或平行线

圆加半径

中点中外线

转图形再看

特殊化

立体几何

长方体、正方体

体积

V=abc

表面积

S=2(ab+ac+bc)

体对角线

L=(a^2+b^2+c^2)的平方根

公式经验结论

FIRST

(ab)(ac)(bc)=(abc)^2

三个不同面的面积之积=（体积）^2

(a+b+c)^2=((a^2+b^2+c^2)d的平方根)^2+2(ab+ac+bc)

(1/4棱长之和)=（L）^2+表面积

((a^2+b^2)的平方根)^2+((a^2+c^2)的平方根)^2+((c^2+c^2)的平方根)^2

=2((a^2+b^2+c^2)的平方根)^2

三个面对角线的平方和=2（L）^2

SECOND

涂色

一个表面涂红色正方体切成N^3

三面涂色的有8块

8个顶点

二面涂色的有12（N—2）块

一面涂色的有6（N-2）^2块

无涂色的（N-2^3）

最短路

l最短=（（a+b）^2+c^2）的平方根

物体位于体对角线两侧

展开图

拼接

切多2面

接少2面

圆柱体

基本公式

V=3.14*r^2*h

S侧=2*3.14*r*h

S全=2*3.14*r*h+2*3.14*r^2

球体

V=4/3*3.14*r^3

V表=4*3.14*r^2

立体几何专题

内切圆与外接圆

长方体

没有内切圆

L=2R外

正方体

2r内=a

R外=3的平方根/2*a

等边圆柱

r=r内

L=2R外

关键

直径=边长

直径=体对角线

平面解析几何

用代数方式处理平面几何问题

特点

公式多，计算烦，两解多

一般方法

待定系数法

实用技巧

反向验证

画草图定性判断

巧解特殊三角形

特殊对称

基本知识

四大公式

中点

（(x1+x2)/2,(y1+y2)/2）

距离

((x2-x1)^2+(y2-y1)^2)的平方根

点到直线距离

d=|Ax0+By0+C|/((A^2+B^2)的平方根)

斜率

定义式k=夹角的正切

k=(y2-y1)/(x2-x1)

注意

x=a 夹角为90度，k不存在

大小比较

|k|越大，直线越贴近y轴

取值范围

直线方程

五种表达式

y=kx+b

y-y1=k(x-x1)

(y-y1)/(y2-y1)=(x-x1)/(x2-x1)

x/a+y/b=1

Ax+By+C=0

求直线方程

设k，可能会漏解x=a

在两坐标轴上截距相等

x/a+y/a=1

y=kx

x/a+y/b=1与坐标轴所围三角形的面积

S=1/2|ab|

圆

一般式

x^2+y^2+Dx+Ey+F=0

表示圆<====>D^2+E^2-4F>0

x^2与y^2的系数相等

圆心为（-D/2,-E/2）

半径为(（D^2+E^2-4F）/4)的平方根

标准式

(x-x0)^2+(y-y0)^2=r^2

圆心（x0，y0）

半径为r

位置关系

点与直线的关系

两直线的关系

设两直线l1:y=k1x+b1，l2:y=k2x+b2

相交k1不等于k2

平行k1=k2且b1不等于b2

重合k1=k2且b1=b2

垂直k1*k2=-1

A1A2*B1B2=0

两直线间的距离d=|C1-C2|/（(A^2+B^2)的平方根）

直线系（过定点）方程

(A1x+B1y+C1)+(A2x+B2y+C2)z=0

必过定点

A1x+B1y+C1=0

A2x+B2y+C2=0

直线与圆的关系

直线l:Ax+By+C=0，圆（x-a）^2+（y-b）^2=r^2

那么圆心M（a,b）到直线l的距离

d=|Aa+Bb+C|/((A^2+B^2)的平方根)

直线与圆相离

d>r

最短距离=d-r

最远距离=d+r

直线与圆相切

d=r

求圆的切线x^2+y^2=a^2

切点在圆上

xx0+yy0=r^2

点在圆外

必有两条（会漏掉x=a的直线）

直线与圆相交

弦长AB=2（（r^2-d^2）平方根）

弦长问题

弦长AB=2（（r^2-d^2）平方根）

点与圆的关系

点（X0,y0），圆（x-a）^2+（y-b）^2=r^2

在圆上

圆（x0-a）^2+（y0-b）^2=r^2

在圆外

圆（x0-a）^2+（y0-b）^2>r^2

在圆内

圆（x0-a）^2+（y0-b）^2

两圆的关系

圆C1:（x-a1）^2+（y-b1）^2=r1^2,圆C2:（x-a2）^2+（y-b2）^2=r2^2

两圆的圆心距d=|C1C2|

相交

|r1-r2|

相交弦长方程：C1-C2

相切

外切

d=r1+r2

内切

d=|r1-r2|

外离

d>r1+r2

圆C1内含在圆C2内

0<=d

解析几何与平面几何综合问题

用解析几何语言给出图形

求平面几何问题

巧解特殊三角形

对称问题

五种特殊对称

方式

点P（x，y）

曲线F（x，y）=0

Ax+By+C=0

关于原点

（-x，-y）

F（-x，-y）=0

A(-x)+B(-y)+C=0

关于x轴

（x，-y）

F（x，-y）=0

Ax+B(-y)+C=0

关于y轴

（-x，y）

F（-x，y）=0

A(-x)+By+C=0

关于y=x

（y，x）

F（y，x）=0

Ay+Bx+C=0

关于y=-x

（-y，-x）

F（-y，-x）=0

A(-y)+B(-x)+C=0

点P（x0，y0）关于直线x+y+m=0的对称点

P'（-y0-m，-x0-m）

点P（x0，y0）关于直线x-y+m=0的对称点

P'（y0-m，x0+m）

画图记忆

点关于直线对称

L0将P1P2连线垂直平分

k(L)*k(P1P2)=-1

P1与P2之中点在L0上

两相交直线对称

三线共点

夹角相等

平移

移动一个特殊点验证

左加右减，上加下减

动点问题

最值问题

轨迹

中点条件：传点

利用平面几何知识

算术

整数

实数

比与比例

数轴与绝对值

数据分析

计数原理与古典概型

图文并茂，动静结合

五大方法

有限少量穷举归纳

用字典序，避免重漏

区分排列还是组合

排列有序，组合无序

准确分类合理分步

分类方法，分步顺序

正难则反除法消序

减法除法，去不满足

特殊条件优先解决

元素位置，位置优先

计数

情况不多

直接穷举

情况个数不多

排列与组合用不上

其他数学知识点综合的问题

情况多

排列组合

摸球问题

摸球的方式

一次性取（无序）

组合

每次取1个（有序）

不放回

样本减少

放回

样本不变

独立的

“一次性取k个球”与“逐次无放回取k个球”

对应结果相同，概率相同

经验结论

抽签中奖与次序无关

袋中有a个中奖的球，b个不中奖的球

逐次无放回抽，则第k次抽到中奖球的概率

a/(a+b)与k无关

前面的k-1不明确

特例：a=1，第k次抽到中奖球的概率为1/（a+b）

取样问题

注意：含与不含；或与且；最大与最小

对象均不同

分房问题

背景

人——每人只能选一间房子

房——房间内可容纳0——N人

经验

n人可进N个房（n<=N）共N^n种（房间数^人数）

n人分别进N个房（n<=N）共{N*(N-1)*(N-2)……}每房间一人

注意

“恰”要选；“指定”不用选

房间中的人数：0，1，2，3……n

区分“人”与“房”

几何问题

与几何有关的计数/概率

平面、解析、空间——古典概率

几何概型

样本点无限个

等可能的

排队问题

排队

直排

特殊要求

位置优先

相邻等间隔，小团体

打包处理——注意包内的顺序

不相邻问题——抽空处理

注意两头的空

定序要求

除法消序

特殊优先

两排问题——直排处理

三元素以上不相邻只能用抽空

环排

n个人环排有（n-1）!种排法

无首无尾，方向无差别

分组分派问题

背景

分组元素不同的，分派的对象

相同

只分组

不同

要分派

注意

先分组再分派

分组：平均/非平均分

分派：定向/非定向

n个组的个数一样，总数/n!

组数问题

背景

三位数，四位数

要求

0不能首位

个位：奇数/偶数，整除

定序

不对应、配对问题

二、三、四元素不对应分别是1，2，9种

涂色问题

乘法原理

某一步如果不确定===>分类

加法原理

按使用颜色个数来分类

相同指标不同对象分配问题——隔板处理

概率

事件间的关系+概率性质和计算

关系

AB、A并B、A-B=A（-B）

公式

0<=P（A）<=1

对立公式

P(-A)=1-P(A)

P(A)=1-P(-A)

减法

P(A-B)=P(A(-B))

=P(A)-P(AB)

特别地

B属于A

===>P(B)<=P(A)

0<=P(A-B)=P(A)-P(B)

加法

两事件

P(A+B)=P(A)+P(B)-P(AB)

特别地

A与B互不相容时，P(A+B)=P(A)+P(B)

三事件

P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)

解题思路

第一步事件的表示

利用概率公式或文氏图求概率

独立性的判定

两事件A、B

关系

A、B互不相容

A、B对立

A、B独立

定义

AB=空集

AB=空集且A并B=U

P(AB)=P(A)*P(B)

概率意义

A、B不能同时发生

A、B不能同时发生；A、B必有一个发生

A事件发生对B事件发生的概率无影响

三事件A、B、C

两两对立

相互对立

P(AB)=P(A)P(B)

A、B、C相互独立

P(AC)=P(A)P(C)

P(BC)=P(B)P(C)

三三独立

P(ABC)=P(A)P(B)P(C)

经验

若A、B、C相互独立

则A-B与C独立

则A-B与BC不一定独立

利用独立性计算概率

P(AB)=P(A)P(B)

关键：复杂事情的分析

n重伯努利概型

要点

每次实验只有2个结果

各种实验中P(A)=p，P（-A）=1-p

n次实验是相互独立的

四种计算

n次实验中A恰好发生k次的概率p

p=(组合n、k)*p^k(1-p)^(n-k) k=0,1,2,……n

n次实验中A至少发生1次的概率p

p=1-(1-p)^n

n次实验中A至多发生1次的概率p

p=1-(1-p)^n+((组合n、1)p^1(1-p)^(n-1)

0次、1次

直到第n次实验A才发生了k次的概率p

p={（(组合（n-1）、（k-1））}p^(k-1)（1-p）^(n-k)*p

={（(组合（n-1）、（k-1））}p^k（1-p）^(n-k)

数据分析

统计量——平均数与方差

定义与意义

平均数

算术平均数

（x1+x2+……xn）/n

中心位置（对称性）

几何平均数

(x1*x2*x3……xn)的n次方根

方差

S^2=1/n((x1-x平)^2+(x2-x平)^2+(x3-x平)^2……(xn-x平)^2)

分散程度

标准差

（S^2）的二次方根=S

注意：两组数据比较

平均数计算

扣定义

加权平均数

巧用对称性

方差

线性变换后数据的均值与方差、标准差

平均数y平=ax平+b

方差S(y)^2=a^2S^2

标准差（a^2S^2）的平方根=|aS|=|a|S

连续5个整数的方差必为2

多组数据的比较：异同，统计意义

统计图表

饼图

可量角计算

频率分布直方图

小距形面积=各组的频率

各小矩形面积之和=1

高中数学

模板简介

猜你喜欢

相关文章